
こんな疑問にお答えします。
この記事を読むメリット
- 振動の計算問題で覚えておくべき公式がわかる
- 過去問の解き方がわかる
私のことを簡単に自己紹介すると、ゼネコンで10年ほど働いていて、一級建築士も持っています。
この記事はだいたい1分くらいで読めるので、サクッと見ていきましょう。
振動で覚えるべき公式

振動の問題で覚えておくべき公式は、固有周期を求める公式です。
固有周期とは、物体固有の揺れやすい周期のことです。
なかなかイメージがつかみにくいかもしれませんが、固有周期で揺らされると共振して揺れやすいとだけ覚えておきましょう。
下記が公式になります。
T=2π√(m/k)
mが質量、kが剛性です。
他は運動方程式(ma=F)やら振動数の式(f=1/T)やら中学校の理科の時間や高校の物理の時間に習った式を使います。
覚えておくべき公式はこれだけなので、すぐに問題を解けそうですね。
2016年一級建築士の構造の過去問
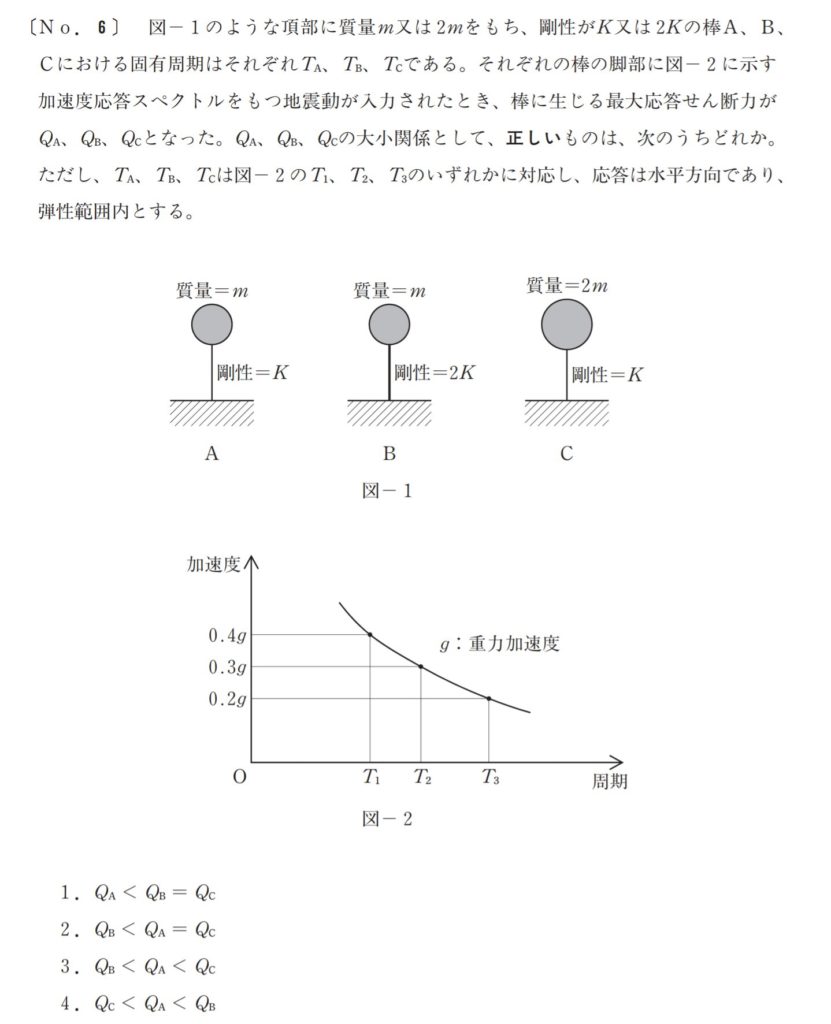
この問題は2016年に出題された一級建築士の構造の問題です。
定期的にこの手の問題は出題されているので、勉強しておけば1点確実に取れます。
それではさっそく過去問を解いて、公式の使い方を確認しましょう。
過去問解説
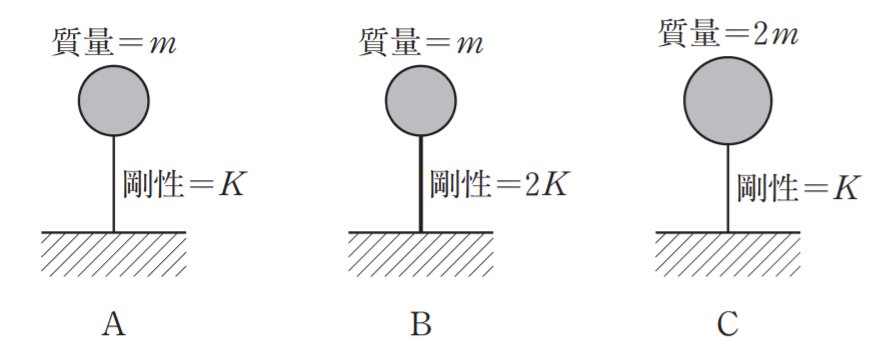
まずはABCそれぞれの固有周期を求めます。
それぞれの固有周期はT=2π√(m/k)に質量mと剛性Kを代入していくだけです。
ですので、
TA=2π√(m/K)
TB=2π√(m/2K)
TC=2π√(2m/K)
となります。
整理すると
TA=T、TB=T/√2、TC=T√2
となるので、TB<TA<TCです。
ここで、固有周期Tがそれぞれ決まった値に応じて加速度が決まるので、
TB=T1より0.4g
TA=T2より0.3g
TC=T3より0.2g
であることがわかります。
それでは、ここからQを求めていきましょう。
運動方程式よりma=Fなので、
QA=m×0.3g=0.3mg
QB=m×0.4g=0.4mg
QC=2m×0.2g=0.4mg
よって1番が正解となります。
計算をしてみると、さほど難しくないことがわかるでしょう。
大切なのは解き方の流れを覚えることです。
一回覚えてしまえば楽勝なので、確実に覚えましょう。
まとめ
この記事では、「一級建築士の構造の試験で振動方程式とか固有周期を計算するんだけど分けわかんなすぎてふるえる」
こんな疑問にお答えしました。
まとめると、公式も少ないので少し対策すればできます。
この記事を参考に、素敵な構造計算ライフをお過ごしください。









