
断面係数とか断面二次モーメントってどうやって計算するんだっけ?
一級建築士の構造の問題で出るから解けるようにならないと
こんな疑問にお答えします。
この記事を読むメリット
- 断面係数が何かわかる
- 断面二次モーメントが何かわかる
- 公式と計算の方法がわかる
私のことを簡単に自己紹介すると、ゼネコンで10年ほど働いていて、一級建築士も持っています。
この記事はだいたい4分くらいで読めるので、サクッと見ていきましょう。
断面係数とは【公式も紹介】

断面係数とは、曲げ応力度が最大となる時のふち応力度を求める係数です。
断面係数の公式

断面係数の公式は下記を覚えておけば良いでしょう。
- M=Z・σ
- Z=I/y
- Z:断面係数、M:曲げモーメント、I:断面二次モーメント、σ:曲げ応力度、y:断面の上下端までの距離
断面係数を求める公式は以下を覚えてください。
- 四角形:bh2/6
- 円:πD3/32
- b:幅、h:高さ、D:直径、π:円周率
断面二次モーメントとは【公式も紹介】

断面二次モーメントとは、断面の曲がりにくさを表す断面定数です。曲げ剛性と決めるとても重要な値になります。
単位はcm4でありヤング係数×断面二次モーメントが曲げ剛性です。
断面二次モーメントの公式

断面二次モーメントの公式は下記を覚えておきましょう。
- 四角形:bh3/12
- 三角形:bh3/36
- 円:πD4/64
- b:幅、h:高さ、D:直径、π:円周率
計算方法は公式に当てはめるだけ

一級建築士の構造の問題で出題されるようなものは、基本的に公式当てはめれば解けます。たまに難問も出ますが、落ち着いて解けば大丈夫です。
では、例題を使って使い方を確認しましょう。
例題【四角形の断面二次モーメントと断面係数を求める】

図のような幅がa、高さが2aの四角形の断面係数と断面二次モーメントを計算してみます。
もうさっそく公式にぶちこみます。
Z=bh2/6
=a×(2a)^2/6
=2a^3/3
I=bh3/12
=a×(2a)^3/12
=2a^4/3
公式にぶちこむだけでちゃんと答えが出ますね。
では、これを応用して問題を解いてみましょう。
例題【H鋼の断面二次モーメントと断面係数を求める】
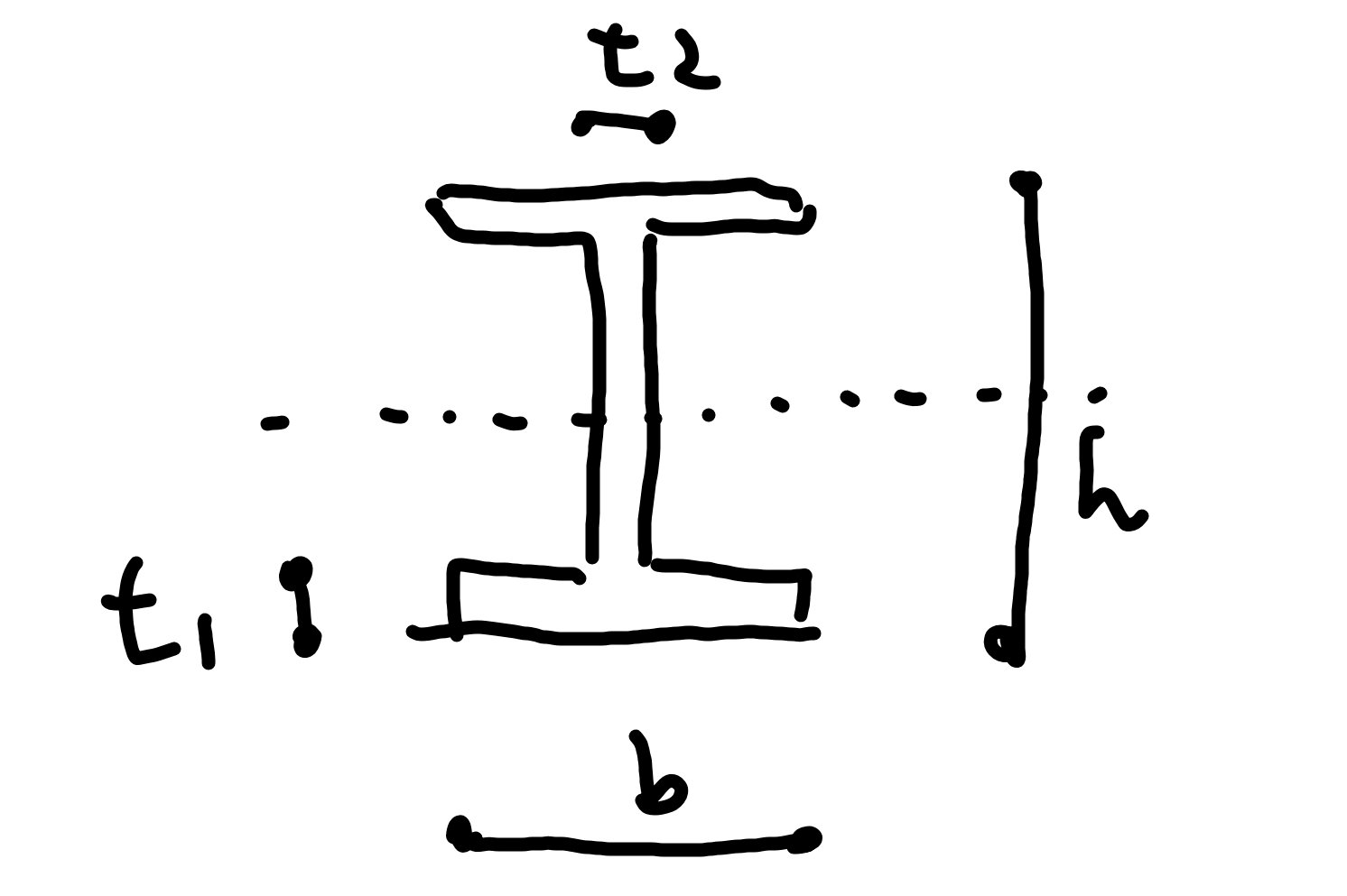
それでは図のようなH型鋼の断面二次モーメントと断面係数を求めてみましょう。
計算方法の解説

基本はやはり公式を使います。
I=bh3/12
=b×(h)^3/12-(b-t2)×(h-2t1)^3/12
Z=I/yなので、
Z={b×(h)^3/12-(b-t2)×(h-2t1)^3/12}/(h/2)
={b×(h)^3-(b-t2)×(h-2t1)^3}/6h
となります。
ここのポイントは、断面二次モーメントは足し算や引き算ができるけど、断面係数はできないという点です。
なので、足し算や引き算が必要な場合は断面二次モーメントを使って断面係数を求めましょう。
令和元年度の一級建築士の構造の過去問
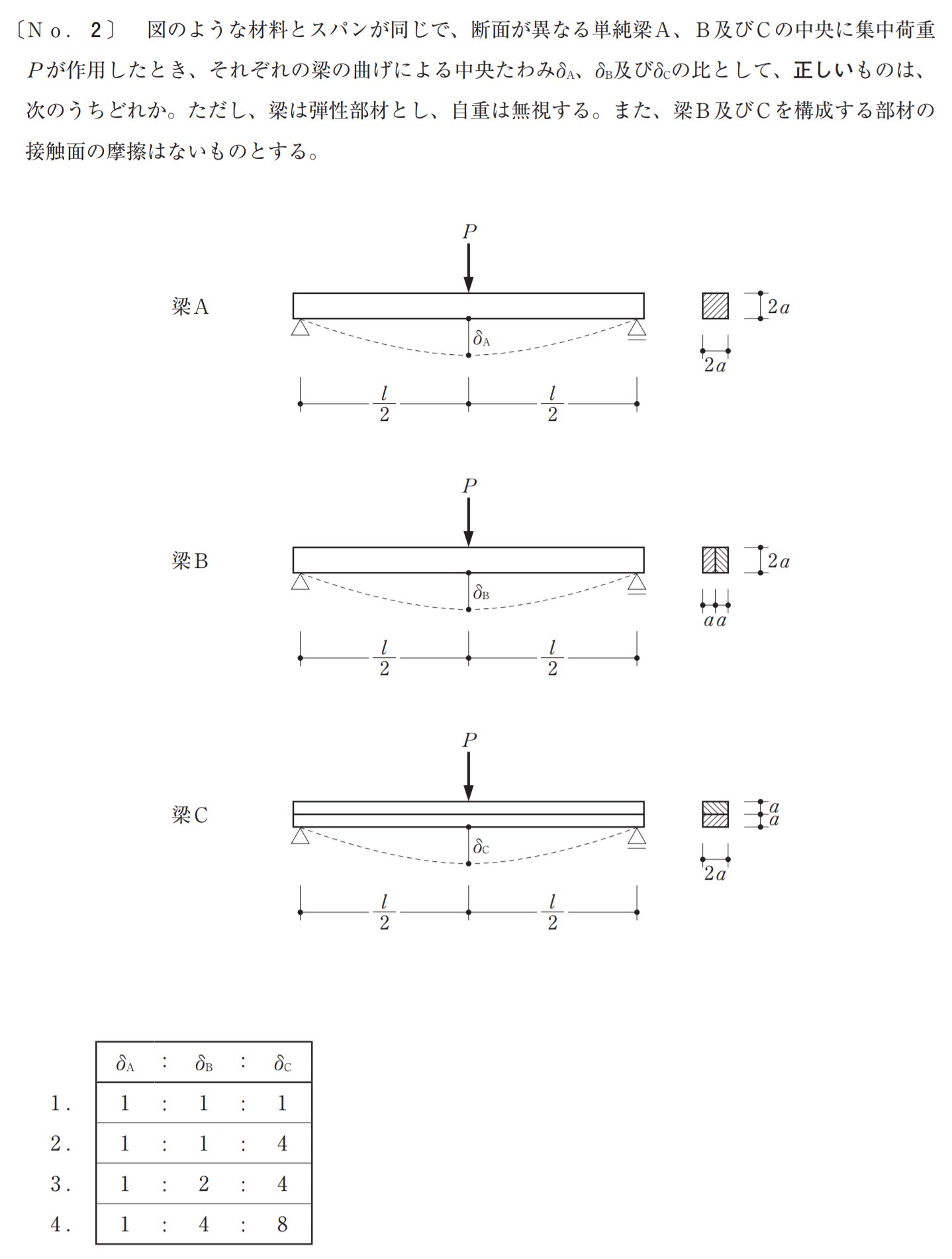
ためしにこの過去問を解いてみましょう。
この問題は断面二次モーメントを理解していないと解けません。
過去問の解説
まず前提の知識として、たわみの公式を覚えておく必要があります。
たわみの公式は
δ=PL3/48EI
です。
部材の長さの3乗に比例し、曲げ剛性に反比例しています。
この問題ではP、L、Eが同じ条件ですので、断面二次モーメントがどうなるのかということを計算すればOKです。
ではAから順に計算しましょう。
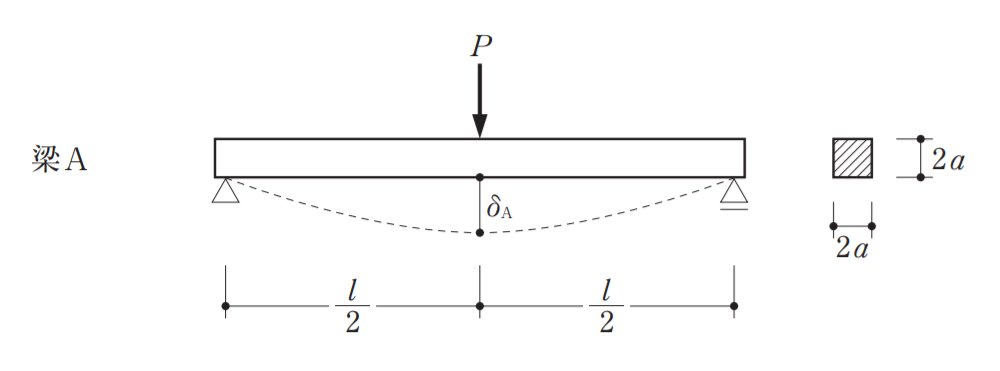
ただ、公式にいれるだけなのでサクサクいきます。
I=bh3/12
=2a×(2a)^3/12=16a^4/12
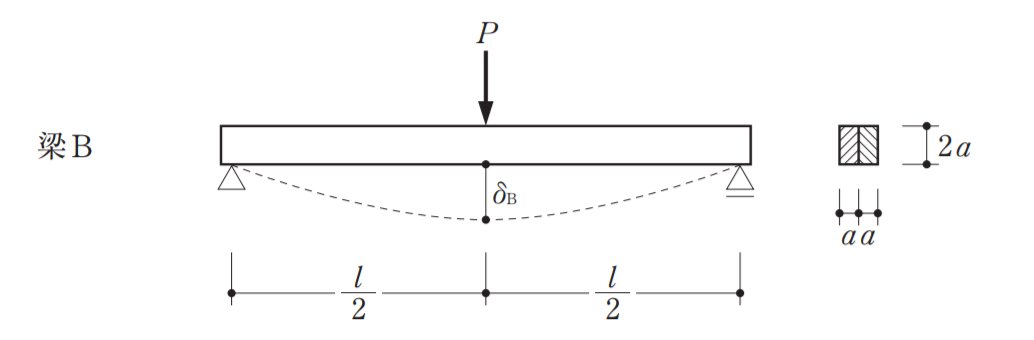
続いてBの断面二次モーメントを計算します。縦に二分割されているので、
I=bh3/12
=a×(2a)^3/12+a×(2a)^3/12
のように2つを足します。ですから、
=2a×(2a)^3/12=16a^4/12
こうなります。
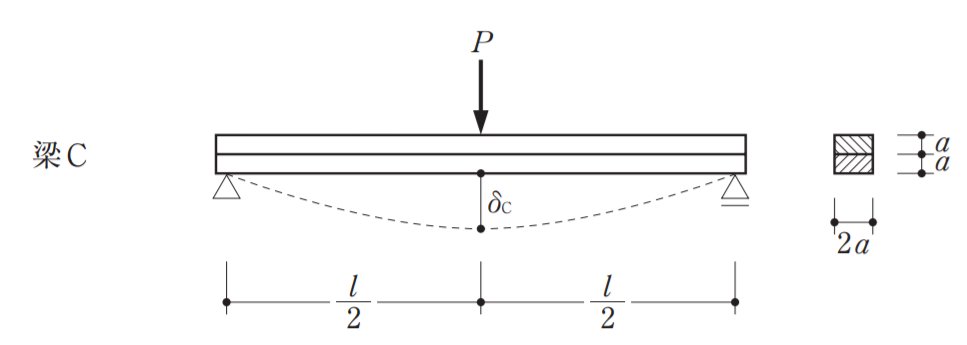
Cの断面二次モーメントを計算します。
Cは横に二分割されているので、hを半分にして足しましょう。
I=bh3/12
=2a×(a)^3/12+2a×(a)^3/12
=4a^4/12
となります。
Ia:Ib:Ic=4:4:1なので、
δa:δb:δc=1/Ia:1/Ib:1/Ic
=1/4:1/4:1=1:1:4
となるので、答えは二番です。
断面二次モーメントの計算方法は理解できましたか?
なれると暗算で解ける問題ばかりなので、繰り返し解いてからだに染み込ませましょう。
まとめ
この記事では、「断面係数とか断面二次モーメントってどうやって計算するんだっけ?一級建築士の構造の問題で出るから解けるようにならないと」
こんな疑問にお答えしました。
まとめると、公式を覚えて過去問を解けば合格できます。
この記事を参考に、素敵な構造計算ライフをお過ごしください。








