
一級建築士の構造で出るから勉強しないわけにもいかないし
こんな疑問にお答えします。
この記事を読むメリット
- 終局耐力の考え方がわかる
- 問題の解き方がわかる
- 公式がわかる
私のことを簡単に自己紹介すると、ゼネコンで10年ほど働いていて、一級建築士も持っています。
この記事はだいたい2分くらいで読めるので、サクッと見ていきましょう。
終局耐力計算の考え方
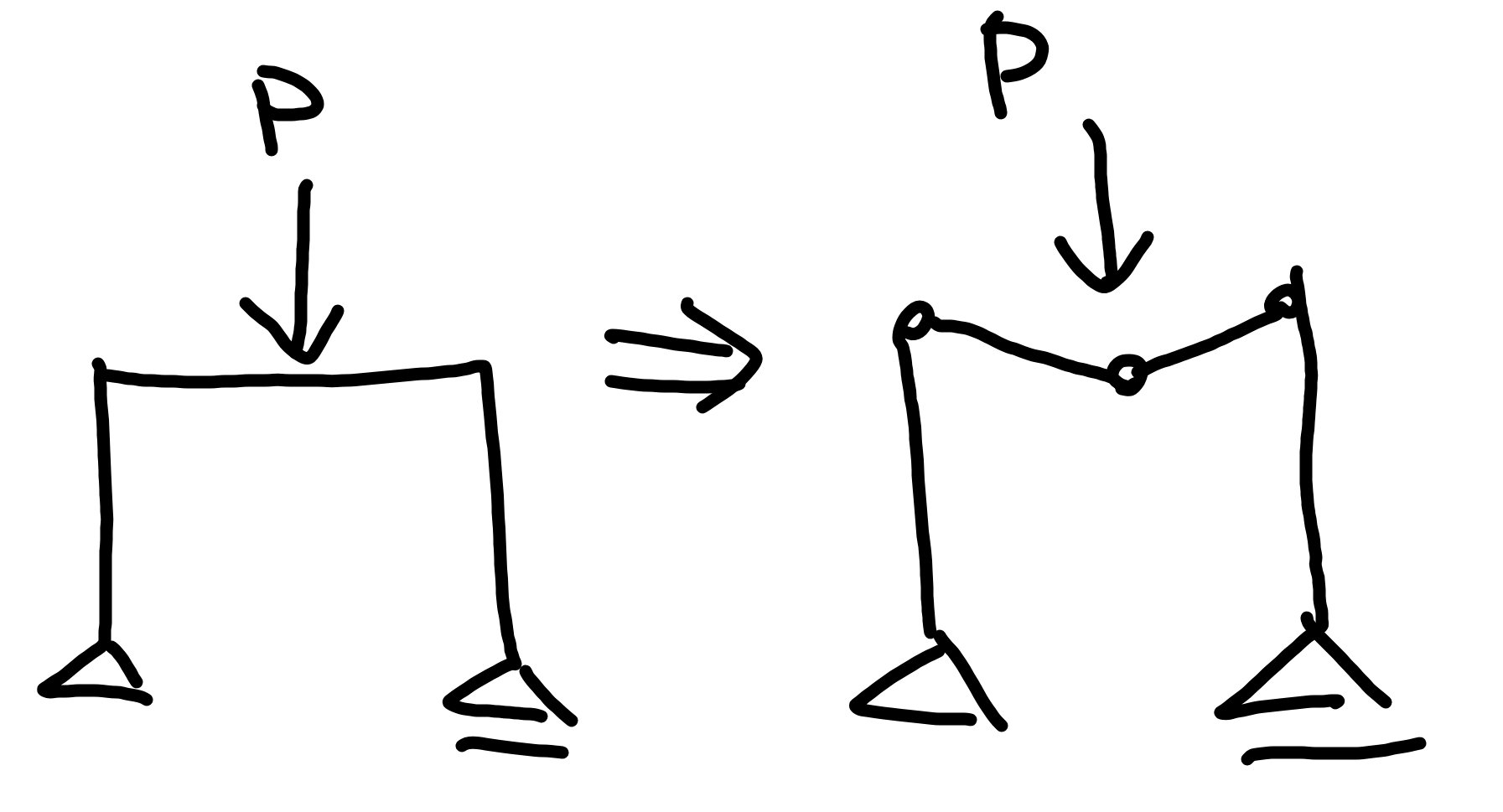
終局耐力は、過度な荷重がかかった時の耐力なのでモデリングが重要になります。
上図のように崩壊した場合、仮想仕事の原理を用いて計算します。
公式は
ΣPδ=ΣMθ
です。
外力の仕事として荷重P×変位δと、内力の仕事としてモーメントM×変位角θが等しくなります。
ちなみにδ=Lθとなるので、注意しましょう。
この式を覚えていないと解けません。
それでは、終局耐力の公式がわかったところで過去問を解いて計算方法を覚えましょう。
2017年一級建築士の構造の過去問
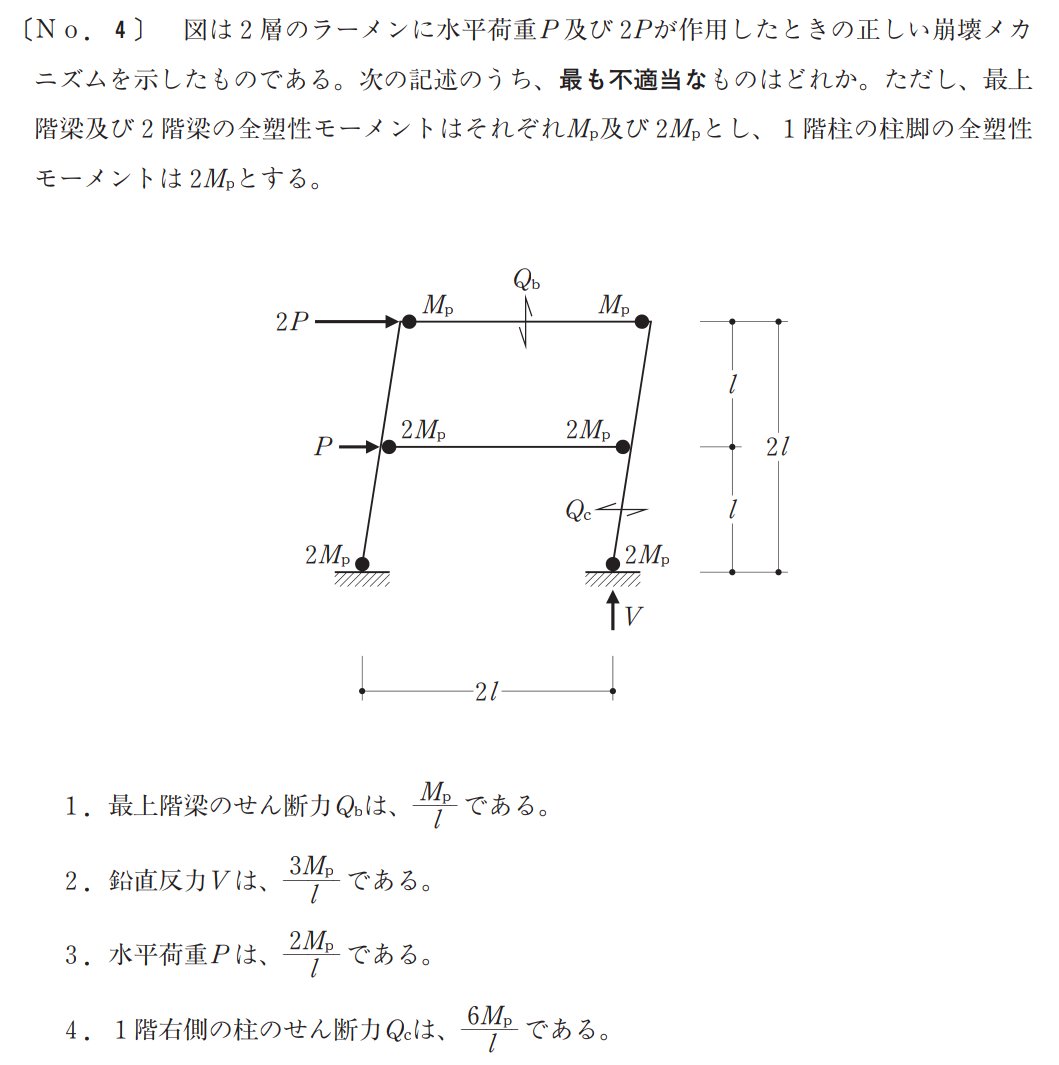
この問題は終局耐力計算の代表的な例ですね。
よく出てるので解き方をしっかりと覚えておきましょう。
ちなみにこのレベルの終局耐力計算は難問です。
過去問解説
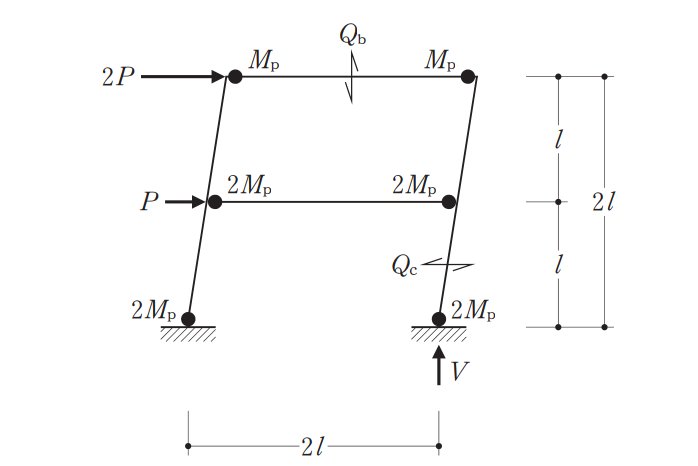
最上階のせんだん力を求めるためにモーメント図を書くとわかりやすいです。
左端が-Mp、右端が+Mpなので、2lで2Mpの傾きとなります。ですので、
Qb=2Mp/2l=Mp/l
よって、1番は正しいです。
下の梁のQもついでにもとめておくと、
4Mp/2l=2Mp/l
になります。
これを足すと3Mp/lとなるので、
V=3Mp/l
です。よって2番は正解になります。
仮想仕事の原理より、
∑(2Puδ1+Puδ2)=2Pu2θl+Puθl=5Puθl
∑(2Mpθ+2Mpθ+Mpθ)×2=10Mpθ
よってPu=2Mp/l
なので3番は正解です。
Qc=3Pu/2=3Mp/l
よって4番は不正解なので、答えは4番となります。
このような難問の問題は上から順に答えを求めていく流れがあるので、全然わからなくても上から順に計算できるとなんとか答えられます。
これぐらい難しい問題が初見で出てきたら正直捨てても良いかもしれませんが、この問題は2013年にも出題されているので、定期的に出題されると思っておいた方が良いでしょう。
2020年か2021年あたりに出題されるかもしれませんね。
過去問をしっかりと解くだけでこの難問も簡単に解けます。
確実に過去問はおさえておきましょう。
まとめ
この記事では、「終局耐力とかわけわかんなすぎて困る。一級建築士の構造で出るから勉強しないわけにもいかないし」
こんな疑問にお答えしました。
まとめると、仮想仕事の原理で計算できます。
難問も過去問をおさえていれば解けるので、確実に過去問を解いておきましょう。
この記事を参考に、素敵な構造計算ライフをお過ごしください。









