
水平剛性の問題ってどうやって解けばいいの?
一級建築士の構造で出るから計算できるようになりたい
こんな疑問にお答えします。
この記事を読むメリット
- 水平剛性で出題される例がわかる
- 計算方法がわかる
私のことを簡単に自己紹介すると、ゼネコンで10年ほど働いていて、一級建築士も持っています。
この記事はだいたい4分くらいで読めるので、サクッと見ていきましょう。
水平剛性の覚えるべき公式

水平剛性で覚えておくべき公式は、たわみの公式です。
特に片持ち梁の公式だけは絶対に覚えていないといけません。
たわみδ=PL3/3EI
という公式ですが、逆にこれを覚えておけば、計算をゴリゴリすれば解けます。
水平変位δ=PH3/6EI
というのも覚えておくと楽ですが、覚えていなくても解けるので余裕が合ったら覚えましょう。
水平剛性の計算の解き方
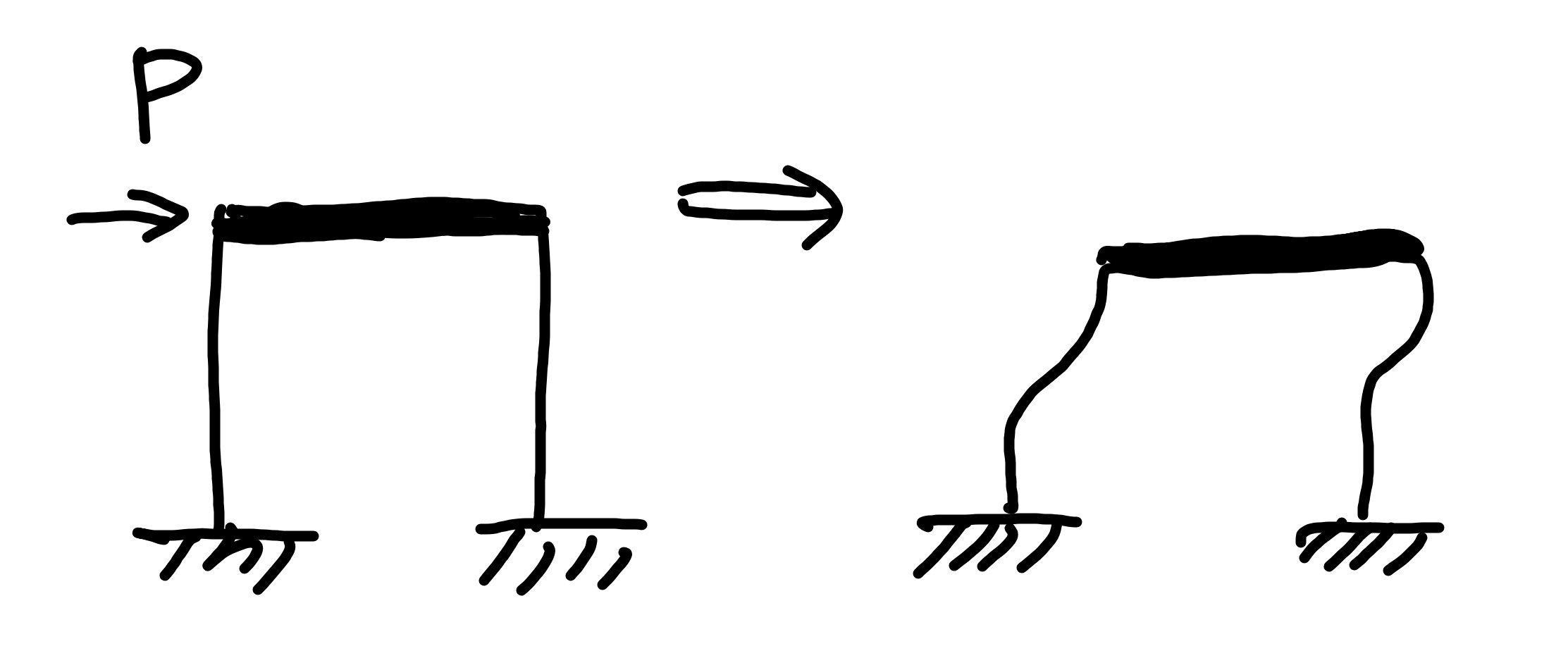
では計算の解き方を考えてみましょう。
水平剛性はそのままだとわかりにくいので、分解して考えましょう。
図のように1階建ての建物に水平力がかかったと考えると、変形を大げさにかくと右図のようになります。
これを拡大すると、下図のようになります。
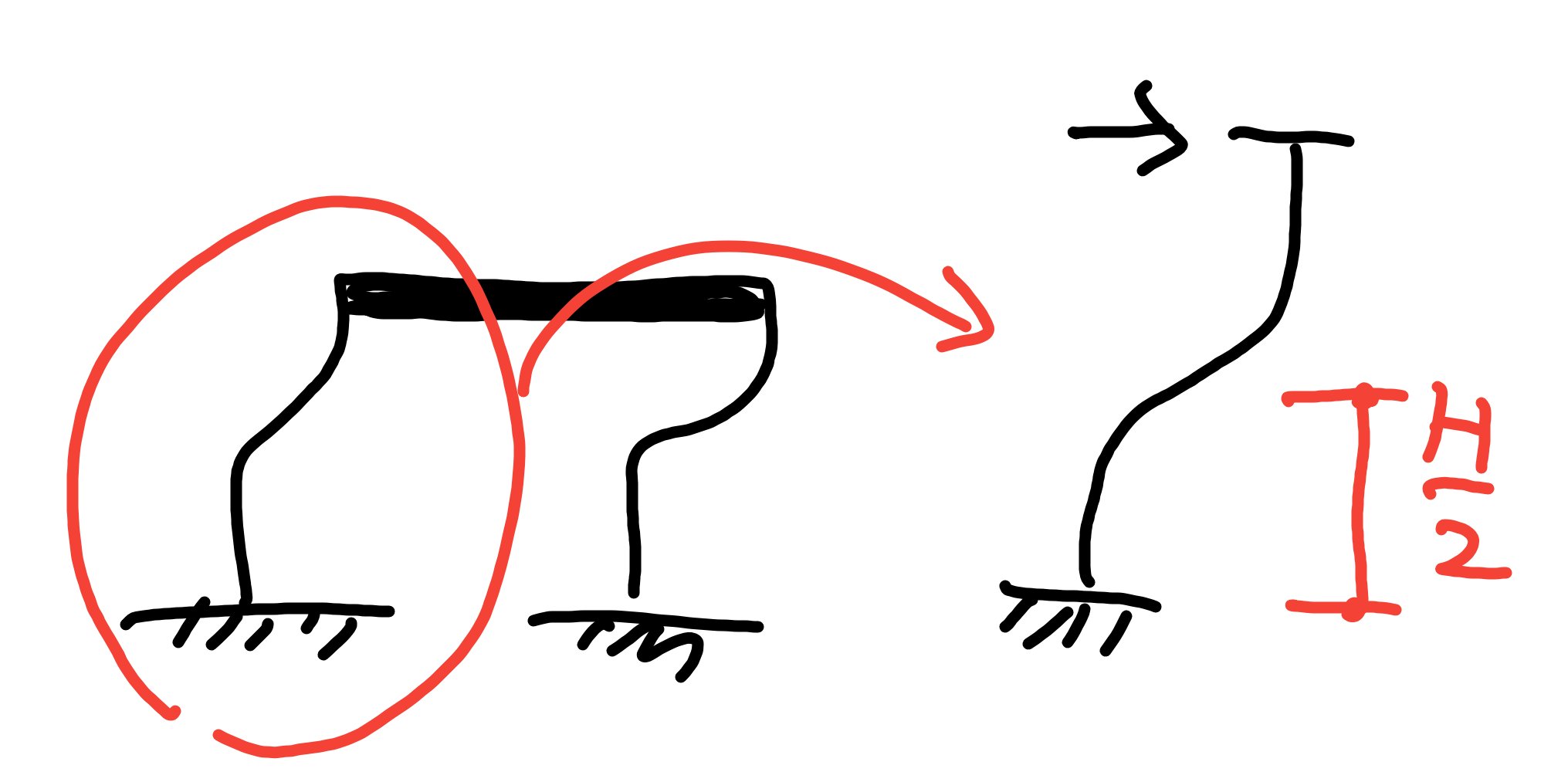
この右図の柱の部分の下半分を見てみると、固定端に集中荷重がかかったと仮定できるのでたわみの公式を使います。
公式はδ=PL3/3EIなので、
δ=2P×(H/2)^3/3EI
=PH3/12EI
です。
下半分の水平変位なので、2倍してPH3/6EIが水平変位となります。
このようにして水平変位を求めるのが水平剛性の問題です。
この考え方で、水平剛性のKを求める問題も出題されます。慣れておくようにしましょう。
2019年一級建築士の構造の過去問
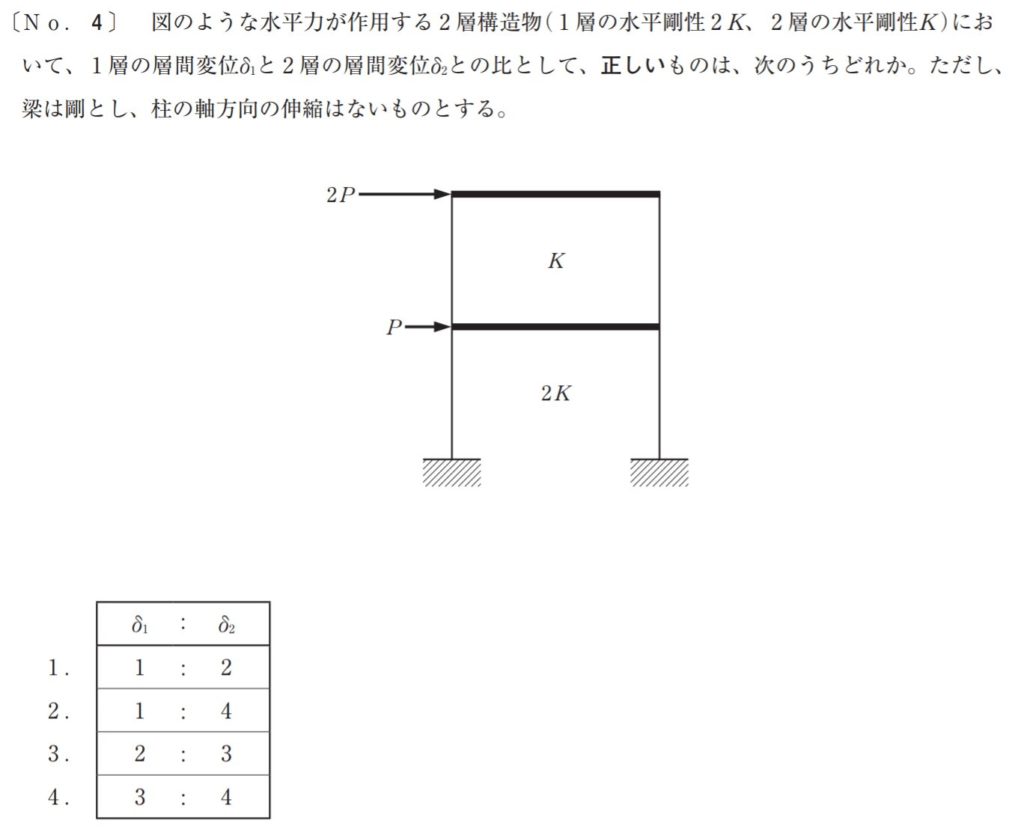
水平剛性の過去問はこのように層間変位を求めるものや、水平剛性Kを求める問題が出題されます。
それではさっそく解いてみましょう。
水平剛性の過去問を解説【たわみを求める】
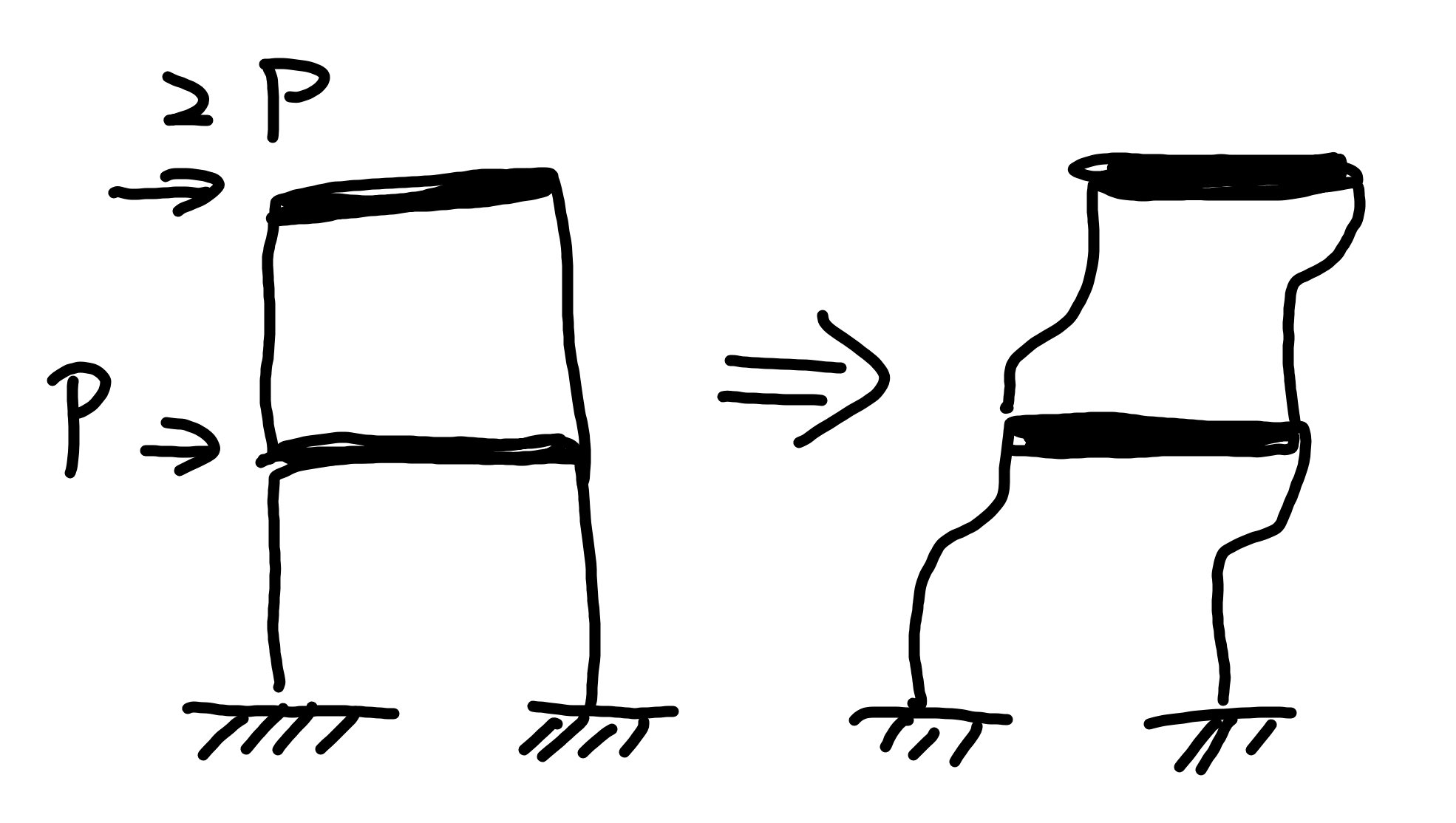
前章で門型の水平変位の計算方法を説明したので、それを利用して解きましょう。
δ2=PH3/6EI
=2PH3/6K
です。
ではδ1も同様に計算するのですが、δ1のPはそのまま使いません。
図のように考えると、フロアにかかる水平力が上部の階から下部にむかって累積されていきます。
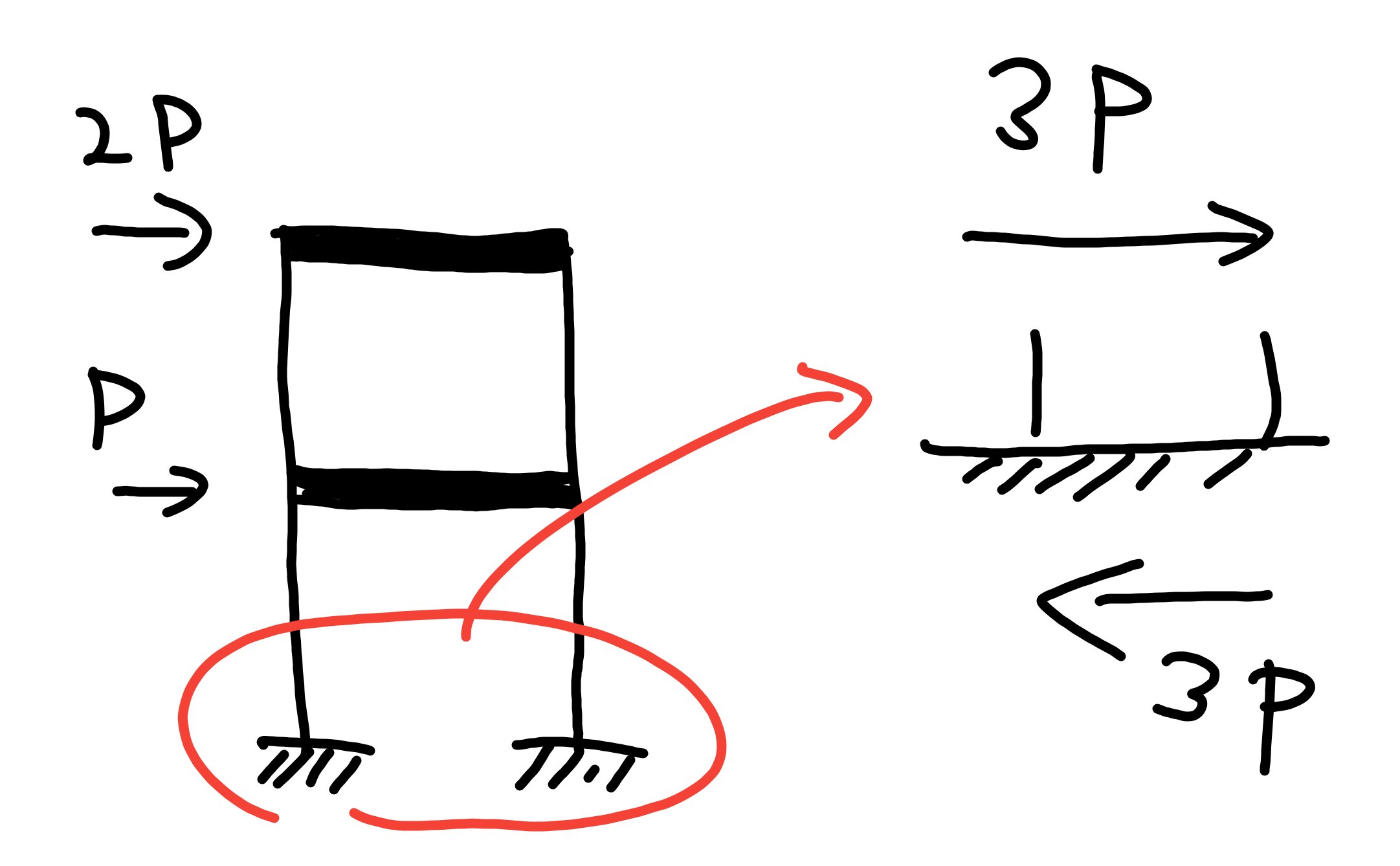
ですので、1層目にかかる水平力は3Pで計算します。
δ1=PH3/6EI
=3PH3/6×(2K)
=PH3/4K
です。
比率を求めると
δ1:δ2=3:4
となるので、答えは4番となります。
私の独自の解き方

ちなみに私はめんどくさいので、これまで説明してきたようなゴリゴリの正攻法で解くことはしません。
計算が得意な方には普通の内容かもしれませんが、せっかくですので解き方をご紹介しておきます。
δ= PH3/6EI
と前章の計算で分かっているので、これをもとに考えます。
δ2はPが2倍、Kが通常なので、
δ2=2δ
δ1はPが3倍、Kが2倍なので、
δ1=3δ/2
となりますので、3:4となります。
こんな感じで解くと計算量も少なくてミスしにくいのでおすすめです。
まとめ
この記事では、「水平剛性の問題ってどうやって解けばいいの?一級建築士の構造で出るから計算できるようになりたい」
こんな疑問にお答えしました。
まとめると、たわみの公式を覚えて解き方を覚えておきましょう。
この記事を参考に、素敵な構造計算ライフをお過ごしください。








