
たわみとかたわみ角ってどうやって計算するんだっけ?
一級建築士の構造の問題で出るから解けるようにならないと
こんな疑問にお答えします。
この記事を読むメリット
- たわみ、たわみ角の公式がわかる
- 過去問の解き方がわかる
私のことを簡単に自己紹介すると、ゼネコンで10年ほど働いていて、一級建築士も持っています。
この記事はだいたい2分くらいで読めるので、サクッと見ていきましょう。
覚えておくべきたわみ、たわみ角の公式

たわみの公式は最低でも4種類覚えておけばOKです。
できれば9種類覚えてほしいですが、やはり最初から全部は難しいので、まずは厳選した6種類をご紹介します。
単純梁の集中荷重
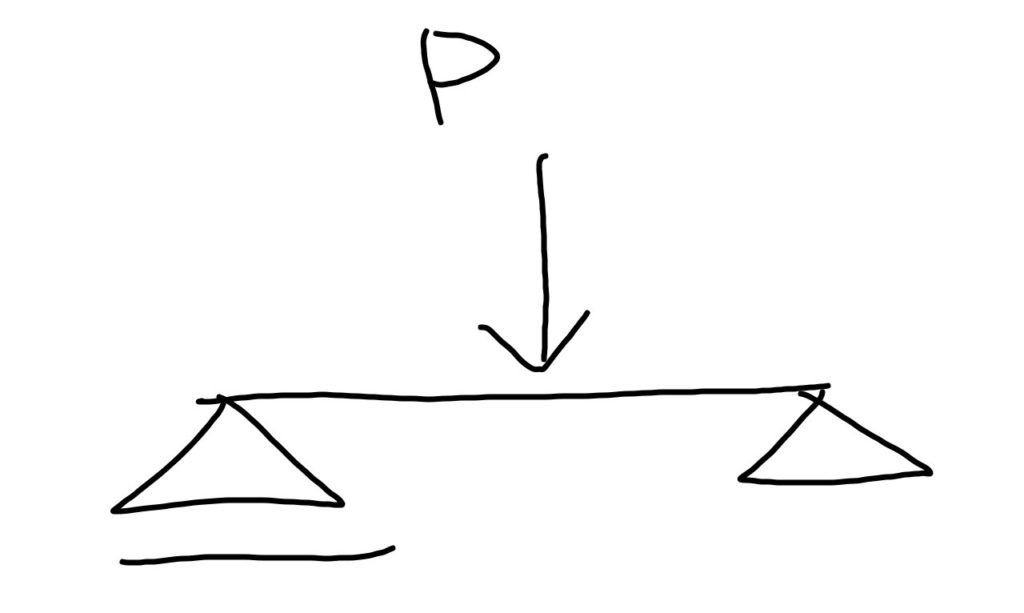
たわみの公式は下記になります。
δ=PL^3/48EI
たわみ角の公式はこちらです。
θ=PL^2/16EI
単純梁の等分布荷重

等分布荷重のたわみの公式はちょっと覚えづらいかもしれません。
δ=5WL^4/384EI
たわみ角の公式は慣れれば覚えられるでしょう。使わないと覚えられません。
θ=WL^3/24EI
片持ち梁の集中荷重

たわみは計算しながら覚えていくのが確実です。
δ=PL^3/3EI
たわみ角は難しい計算問題の時によく使われています。
θ=PL^2/2EI
片持ち梁の等分布荷重
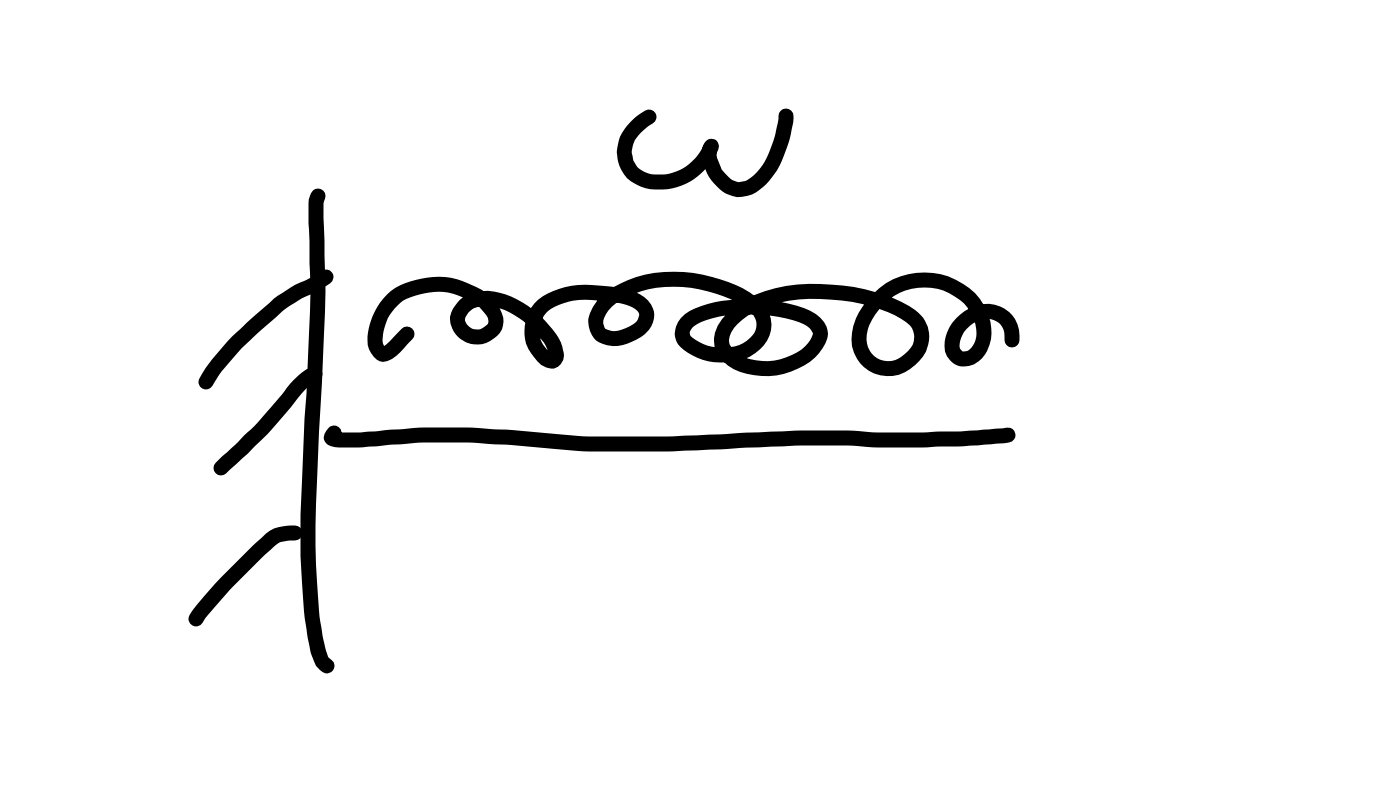
片持ち梁の等分布荷重は自重によるたわみを再現するのに使いやすいですね。
δ=WL^4/8EI
たわみ角は慣れるまで何度も問題を解きましょう。解けば覚えます。
θ=WL^3/6EI
両端固定の集中荷重
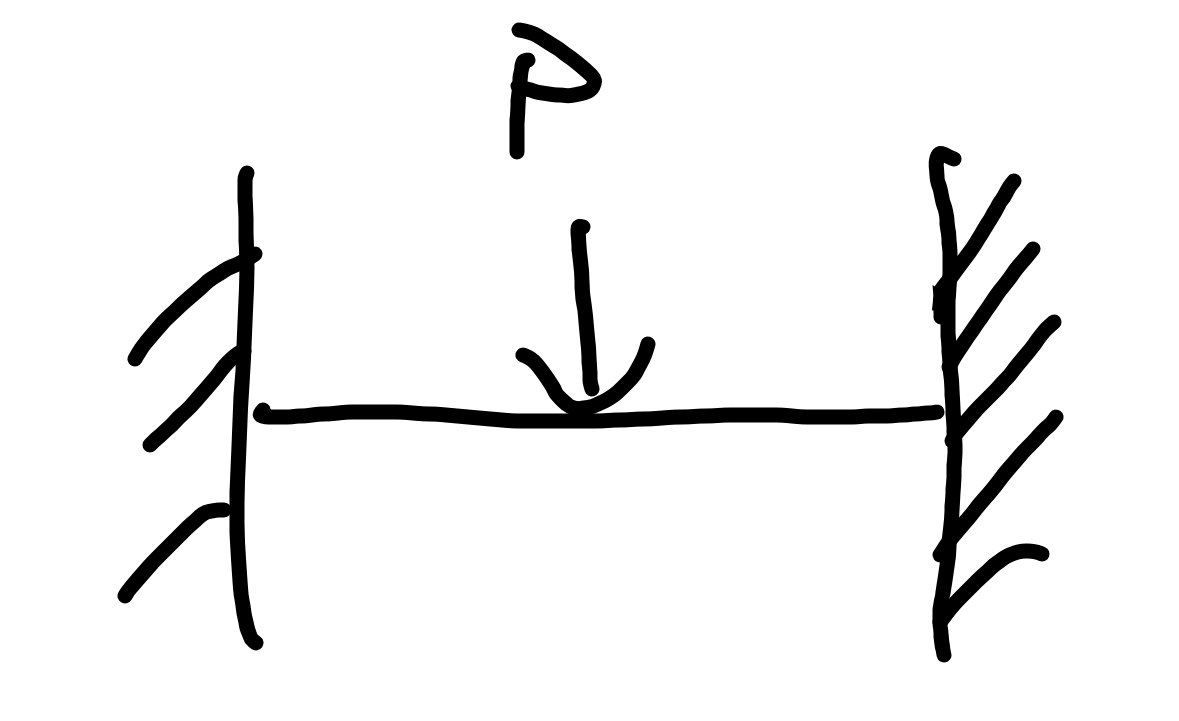
両端固定の時はいわゆるRCラーメン構造が該当します。
δ=PL^3/192EI
なかなか不静定の問題を解くのは難しいですが、現実の構造は不静定が多いです。確実に覚えましょう。
固定端なので、たわみ角は
θ=0
両端固定の等分布荷重

これで6つ目のたわみの公式です。
δ=WL^4/384EI
両端固定の場合は中心部のたわみ角は0になります。
θ=0
これくらいの公式を覚えておけばだいたい対応できるので覚えておいてください。
2018年の一級建築士の構造の過去問
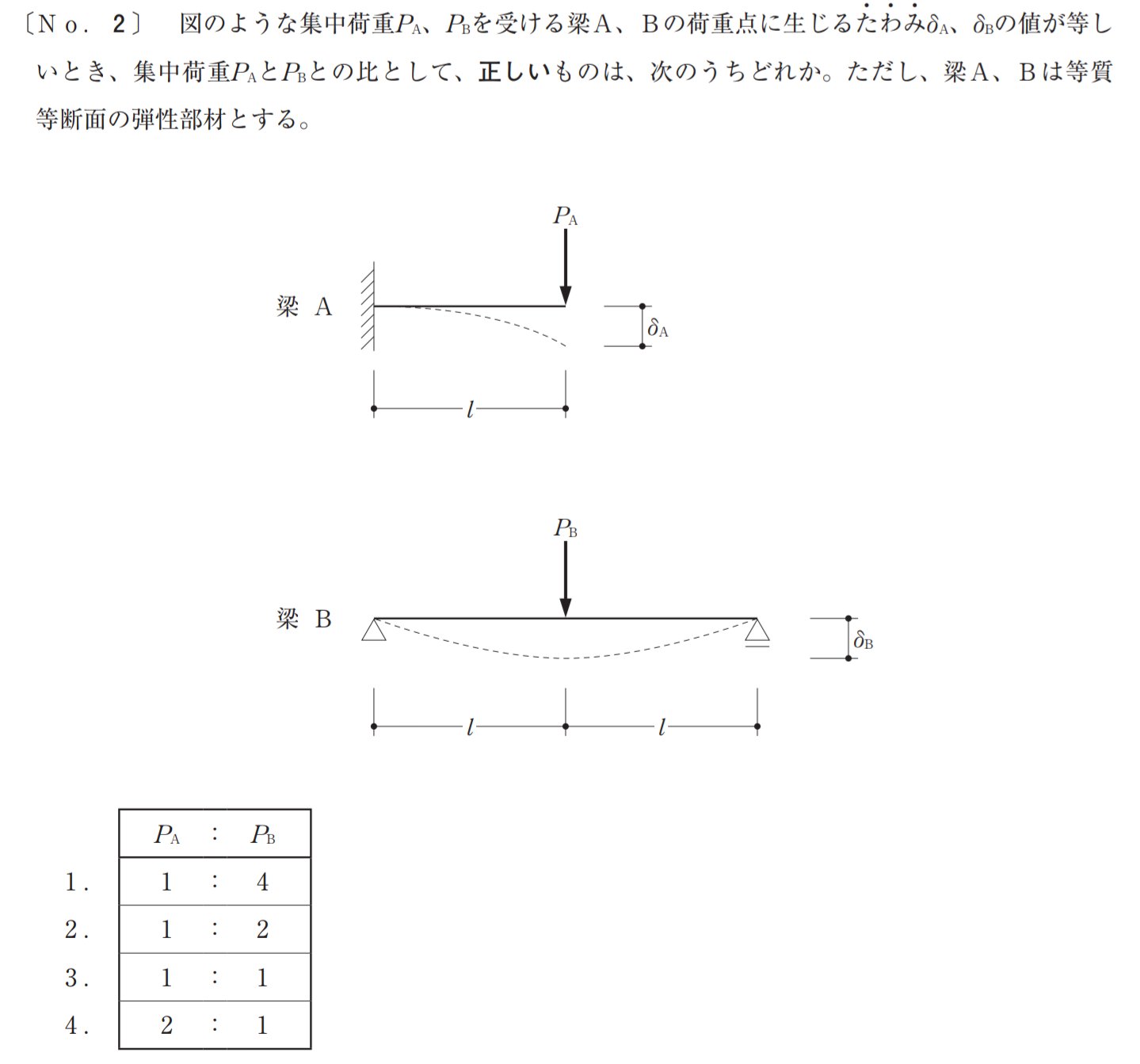
さきほど覚えた公式を使ってこの過去問を解いてみましょう。
過去問の解説
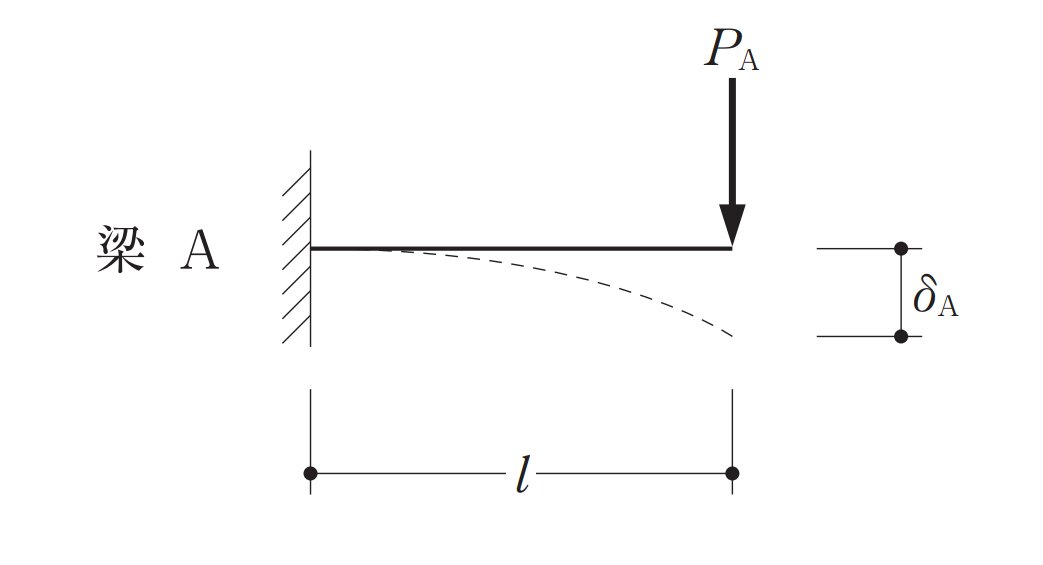
まずAの梁のたわみを公式でもとめます。公式そのままなので、難しくありません。
δa=PaL^3/3EI
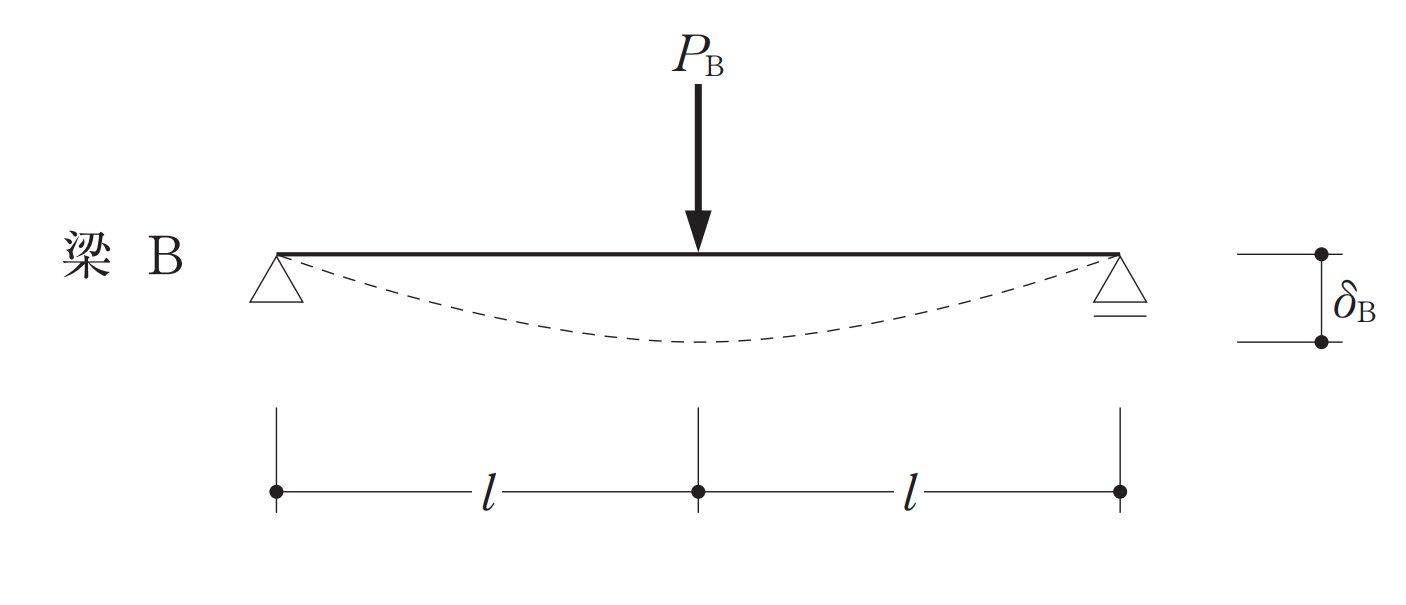
一方でBの梁は長さが少し長いので公式に代入します。
δb=PbL^3/48EI
=Pb(2L)^3/48EI
=PbL^3/6EI
となります。
δa=δbなので
PaL3/3EI=PbL3/6EI
Pa=Pb/2
です。よって答えは二番になります。
公式を覚えてるだけで解けるサービス問題なので、確実に公式を覚えるようにしましょう。
まとめ
この記事では、「たわみとかたわみ角ってどうやって計算するんだっけ?一級建築士の構造の問題で出るから解けるようにならないと」
こんな疑問にお答えしました。
まとめると、公式を覚えて過去問を解けば合格できます。
この記事を参考に、素敵な構造計算ライフをお過ごしください。








