
必要な公式も良く分からないし
こんな疑問にお答えします。
この記事を読むメリット
- 到達モーメントと分割モーメントのルールがわかる
- 覚えるべき固定端モーメントがわかる
- 一級建築士の構造で出題された不静定の過去問の解き方がわかる
私のことを簡単に自己紹介すると、ゼネコンで10年ほど働いていて、一級建築士も持っています。
この記事はだいたい1分くらいで読めるので、サクッと見ていきましょう。
分割モーメントと到達モーメント
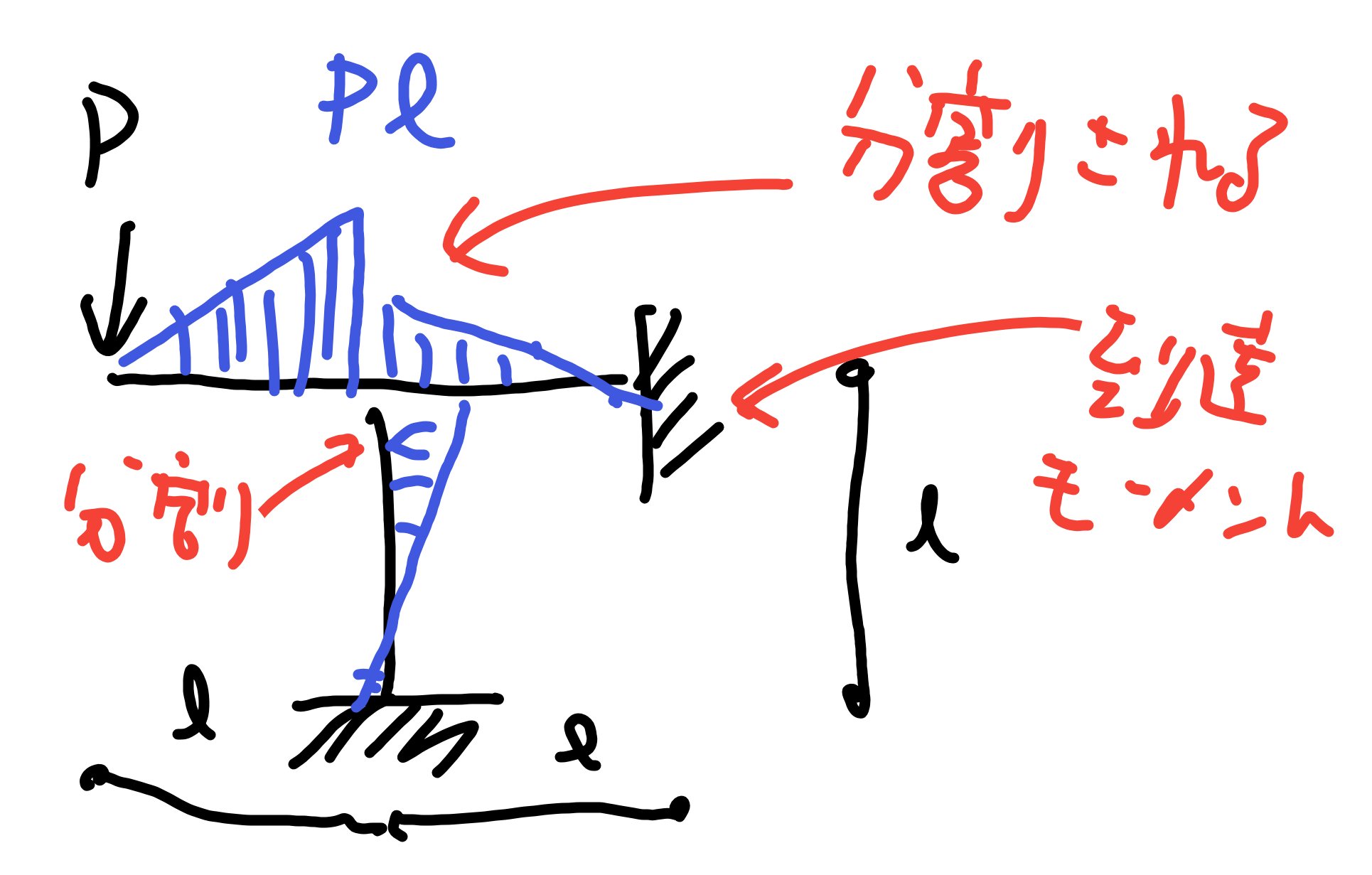
分割モーメントとは、接点に繋がる部材が複数ある場合に分割して伝わるモーメントです。
部材の剛性の比に応じて、モーメントが振り分けられます。
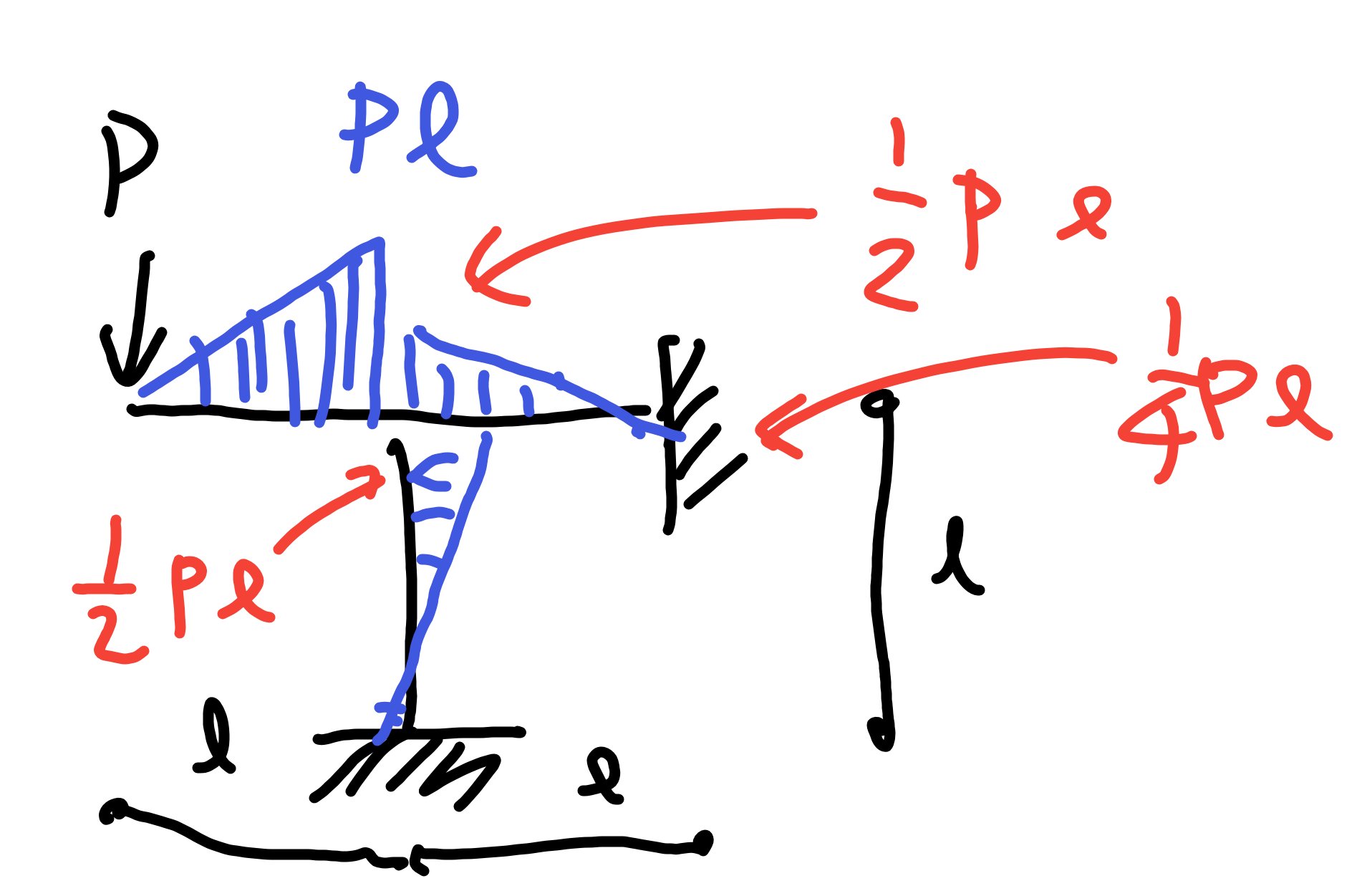
到達モーメントとは、各部材に振り分けられたモーメントが他の端部に伝わるモーメントです。
上図のように剛性に応じて振り分けられます。
固定端では、到達モーメントは分割モーメントの1/2になります。
集中荷重の場合の固定端モーメント
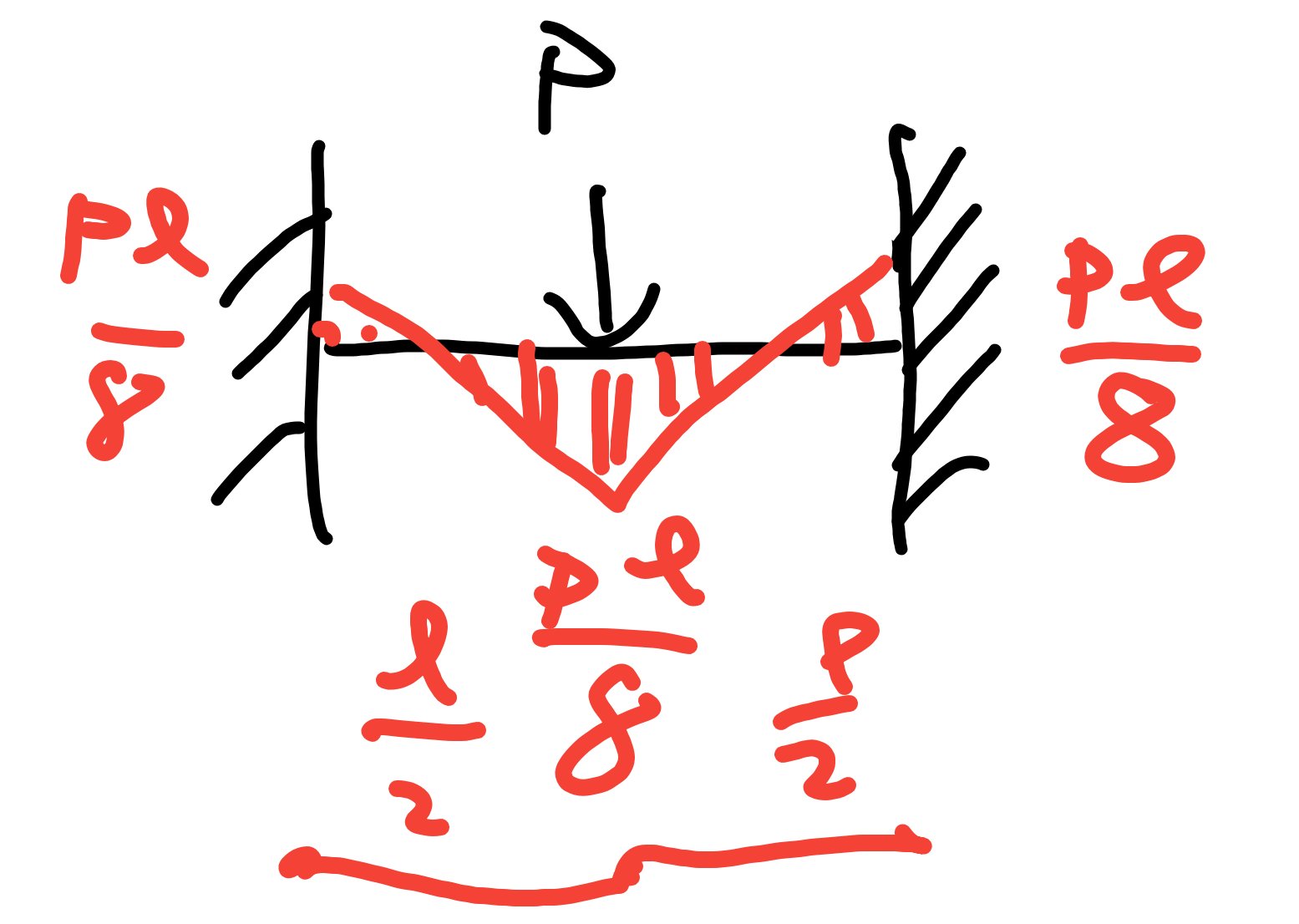
集中荷重の固定端モーメントは上図のようになります。
中央部、両固定端部でモーメントはPL/8です。
等分布荷重の場合の固定端モーメント
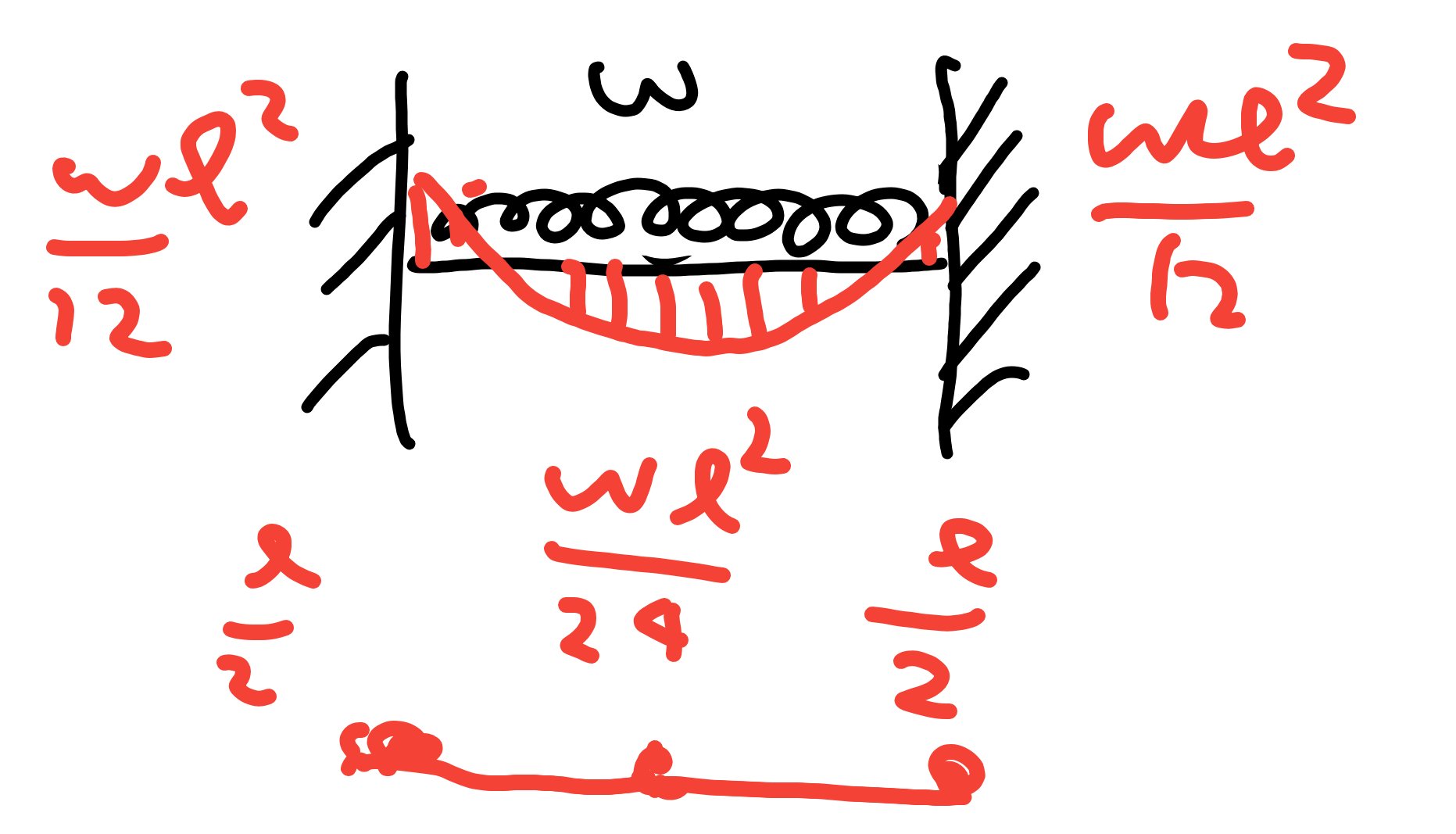
等分布荷重の場合、モーメントは両固定端部でwL2/12、中央の最大部でwL2/24となります。
ルールってこれくらいしかないんですよね。
なので、サクッと覚えて問題を解けるようになりましょう。
2019年一級建築士の構造で出題された過去問
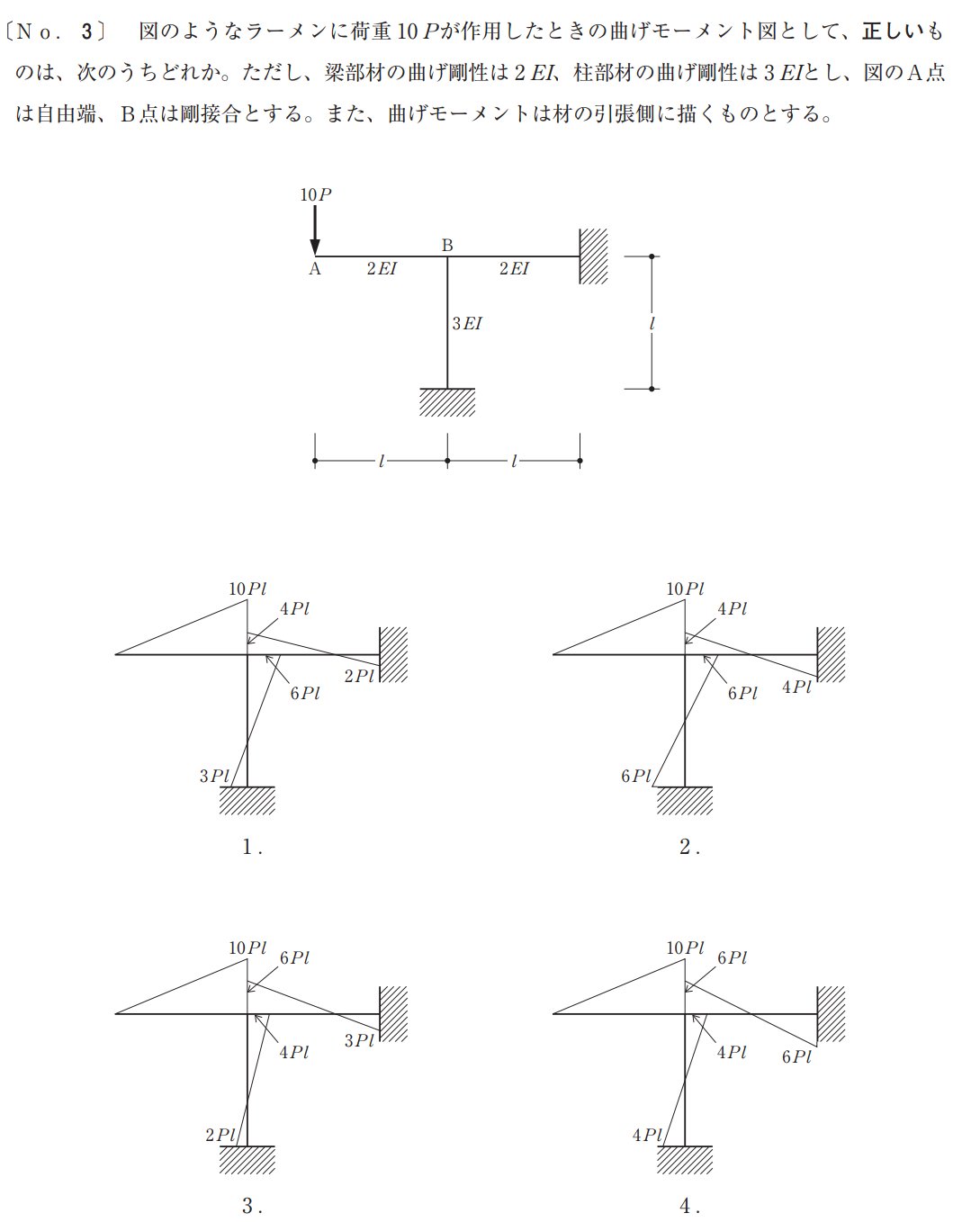
ではさっそく過去問を解いていきましょう。
この問題は一級建築士の構造で出題された不静定の応力を求める問題です。
この問題は、分割モーメントと到達モーメントを理解しているかを問われています。
計算もさほどむずかしくありません。
良く出題されているので、しっかりと解き方を覚えましょう。
過去問解説

まず到達モーメントから見てみましょうか。
到達モーメントは固定端の場合分割モーメントの半分になります。
ですので、半分になっている1番か3番が正解です。
次に分割モーメントを求めましょう。
下の棒の剛性は3EI、右の棒の剛性は2EIですので、モーメントも3:2にわりふります。
ですので、下の棒に6PL、右の棒に4PL割り振るのが当たりです。
よって答えは1番となります。
全然計算してないですよね?
計算しなくても計算問題は解けるので、苦手だからといって捨てるのはもったいないです。
得点源となるので確実にものにしましょう。
まとめ
この記事では、「不静定の計算って何をどうすれば良いかわからないなぁ。必要な公式も良く分からないし。」
こんな疑問にお答えしました。
まとめると、ちょっとしかルールは無いので、それ覚えて計算の流れを覚えましょう。計算も驚くほどありません。
この記事を参考に、素敵な構造計算ライフをお過ごしください。









