
どうやったら計算できるの?
こんな疑問にお答えします。
この記事を読むメリット
- 全塑性モーメントの公式がわかる
- 全塑性モーメントの計算方法がわかる
私のことを簡単に自己紹介すると、ゼネコンで10年ほど働いていて、一級建築士も持っています。
この記事はだいたい2分くらいで読めるので、サクッと見ていきましょう。
弾性、弾塑性、塑性のモーメントは何が違うのか
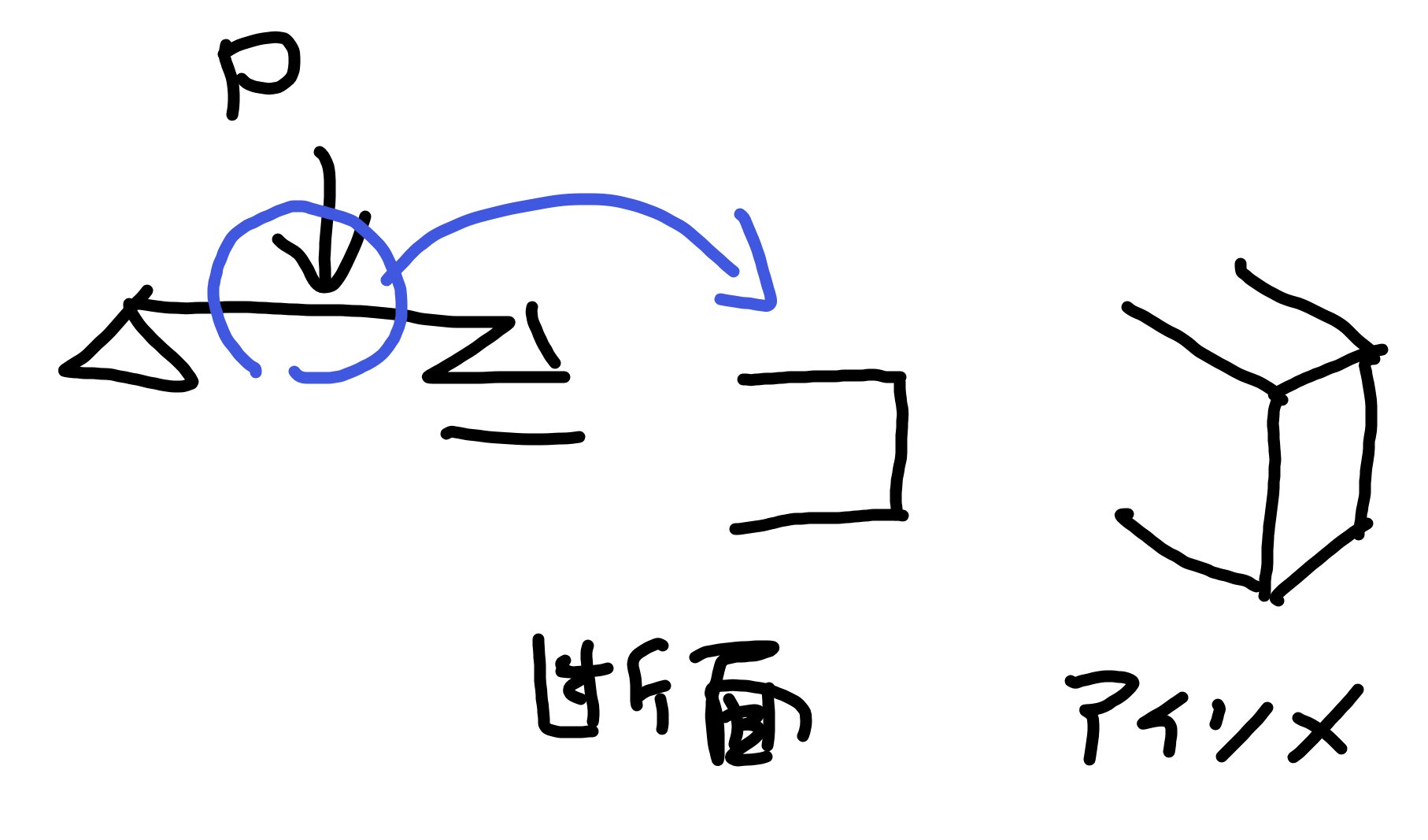
結論をいうと、弾性、弾塑性、全塑性モーメントは部材の応力の形状が変わります。
上図のように集中荷重が作用した場合の応力を、部材を拡大してみてみましょう。
弾性モーメント
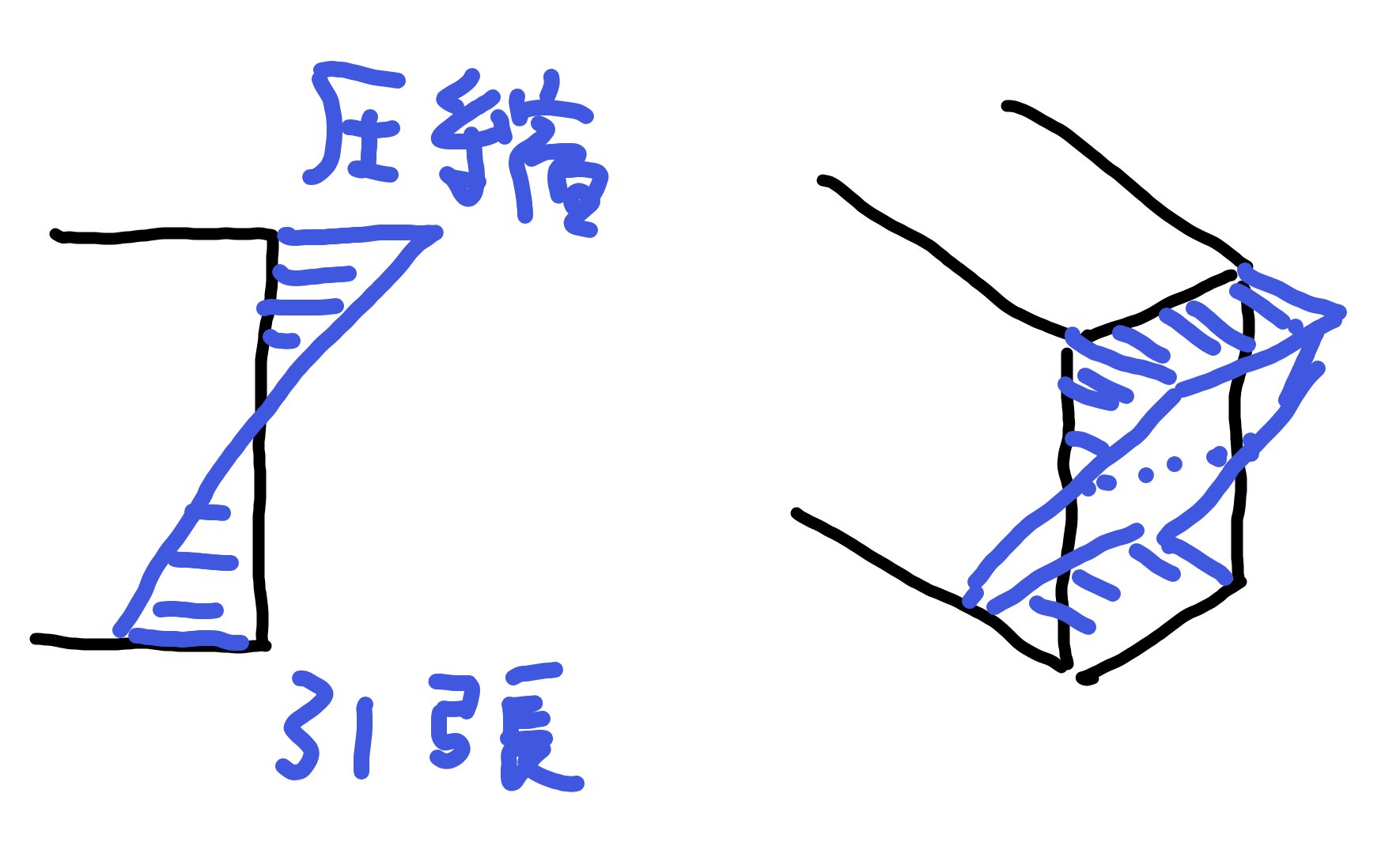
弾性の場合は部材のモーメント図が上図のようになります。
三角形の大きさに多少の差はあれど、形は同じです。
弾塑性モーメント
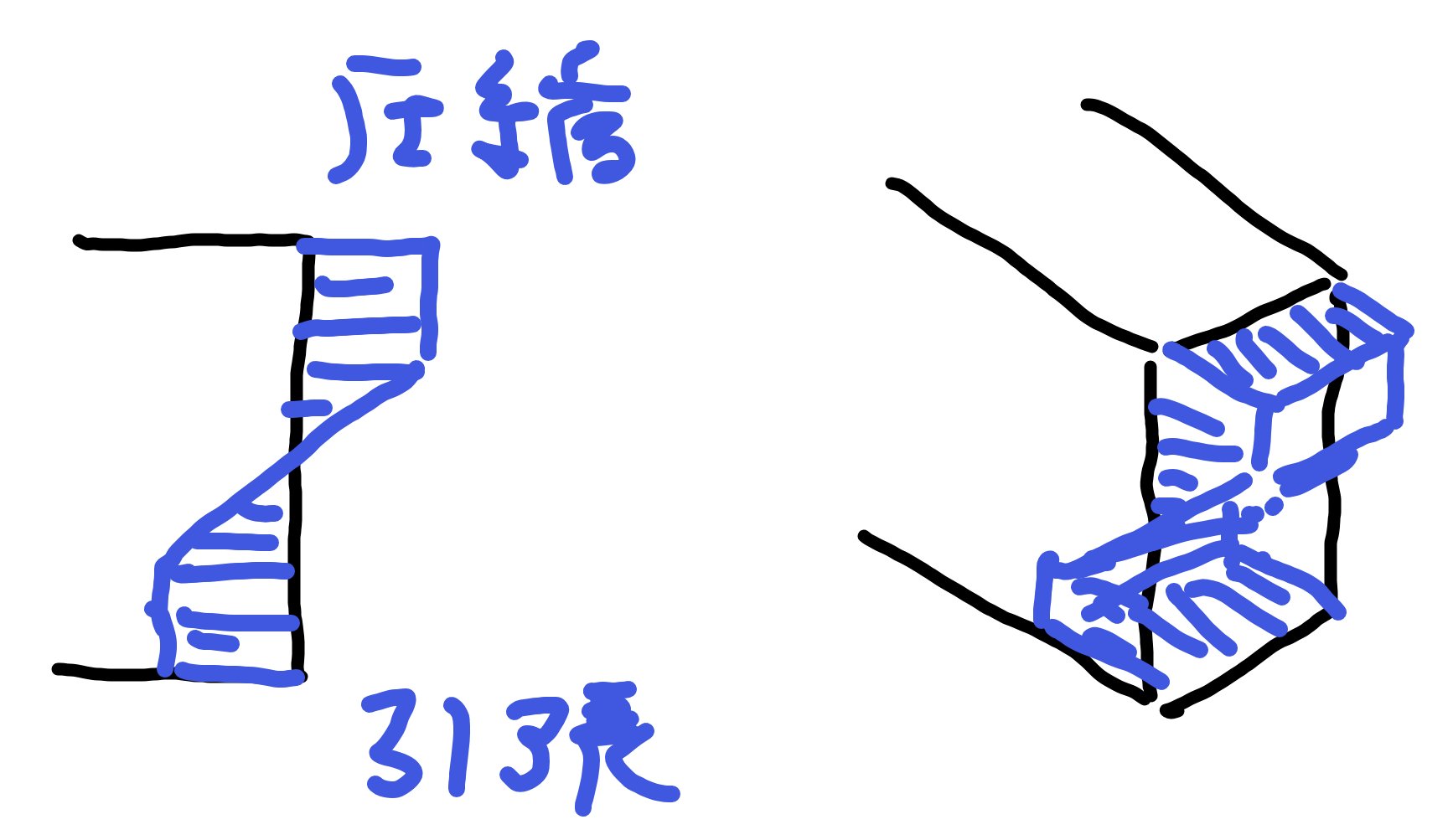
弾塑性の場合は一部が塑性し始めているが、まだ弾性の範囲も残っています。
なので、三角形が図のように台形状になるのです。
分割して長方形部が塑性部、弾性部分が三角形部になります。
全塑性モーメントの考え方
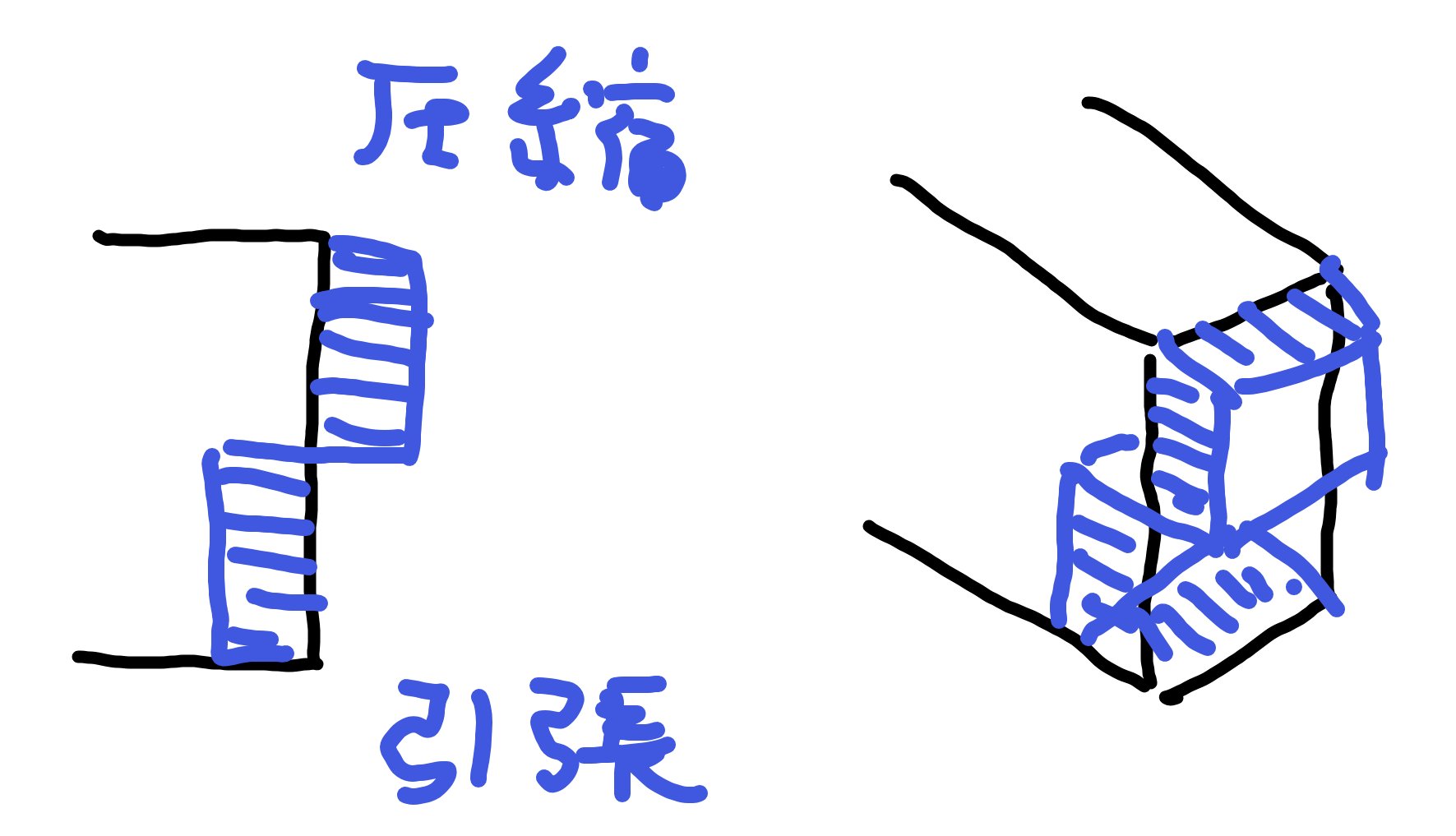
では全塑性モーメントはどうなるのかというと、三角形だった部分が全て四角形になります。
公式は
全塑性モーメントMp=σy×Zp
となりますが、これは
σ=M/Z
をただ変えただけですね。
そんなに難しくないのでさくっと覚えてしまいましょう。
一応こんな公式がありますが、Zpの意味合いは圧縮部四角形の面積×圧縮と引っ張りの距離なので、高さD、幅Bとすると、
(B×D/2)×(D/4+D/4)=BD2/4
となります。
この流れは覚えておきましょう。
2019年一級建築士の構造の過去問
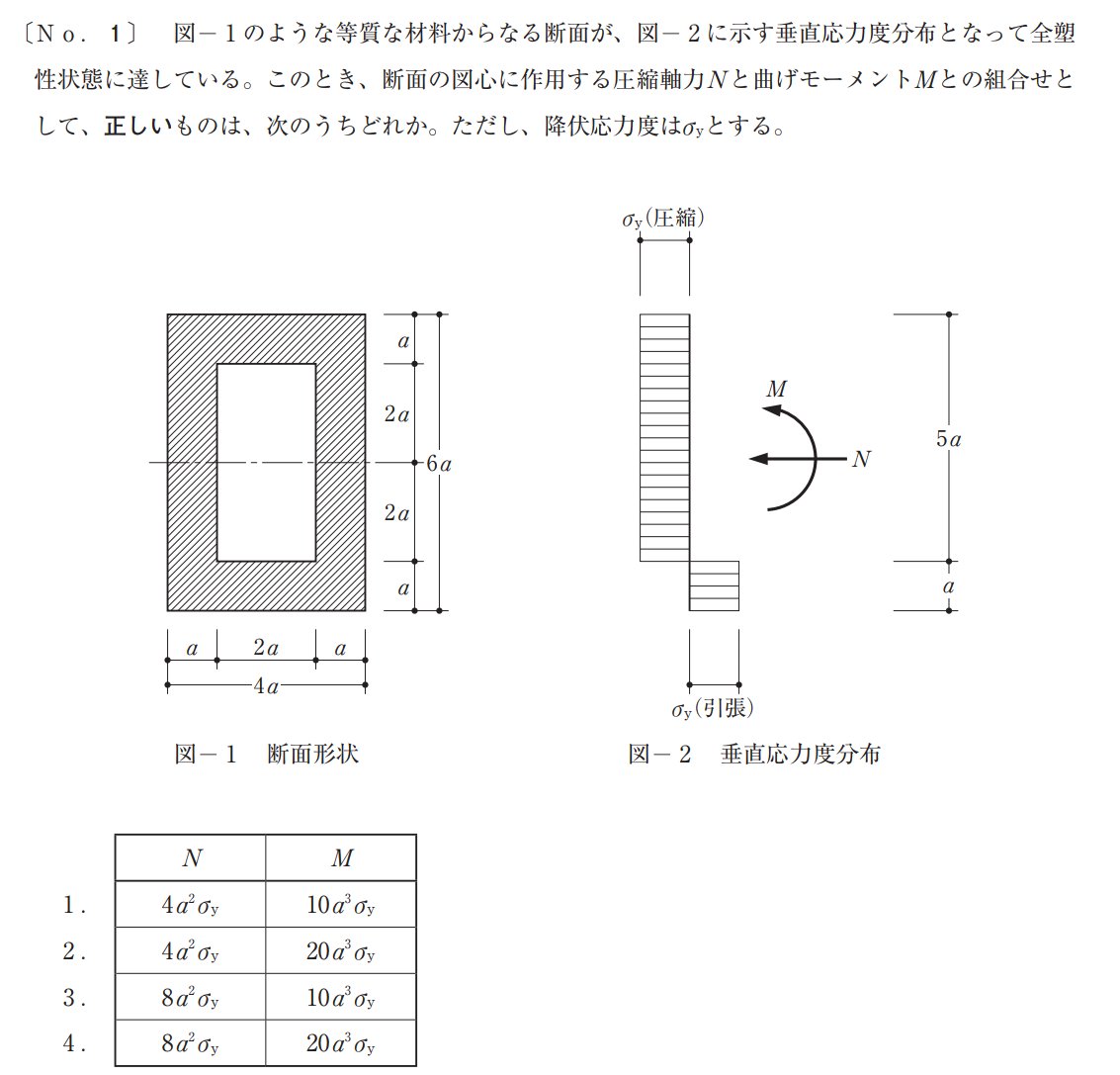
まずこちらの過去問を解いてみましょう。
見たところ、全塑性モーメントを求める問題のようですね。
さきほど覚えた公式を使って解説します。
過去問を解説
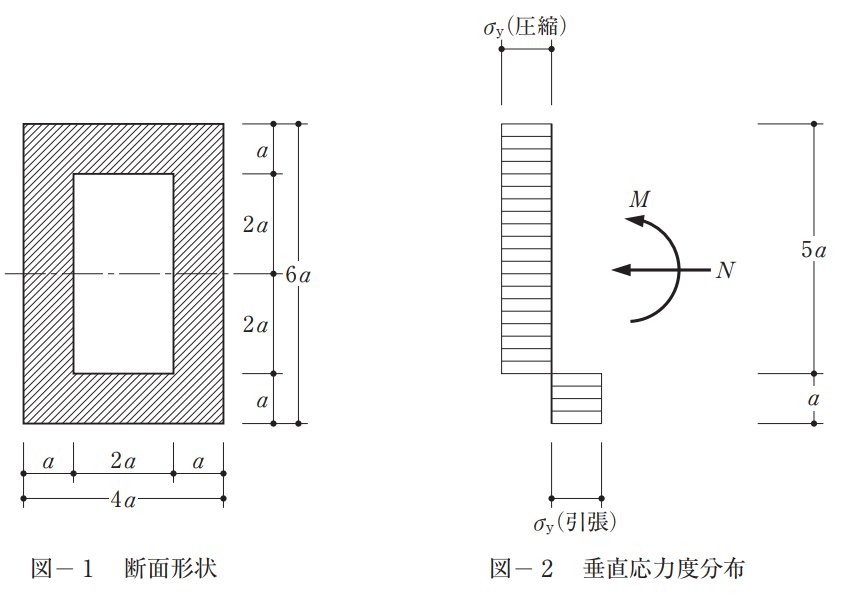
まずNの大きさを求めます。
引張の形状を見ると、Mの圧縮部分は上からaの部分だけとなるので(下図赤)Nは下図の青の部分です。
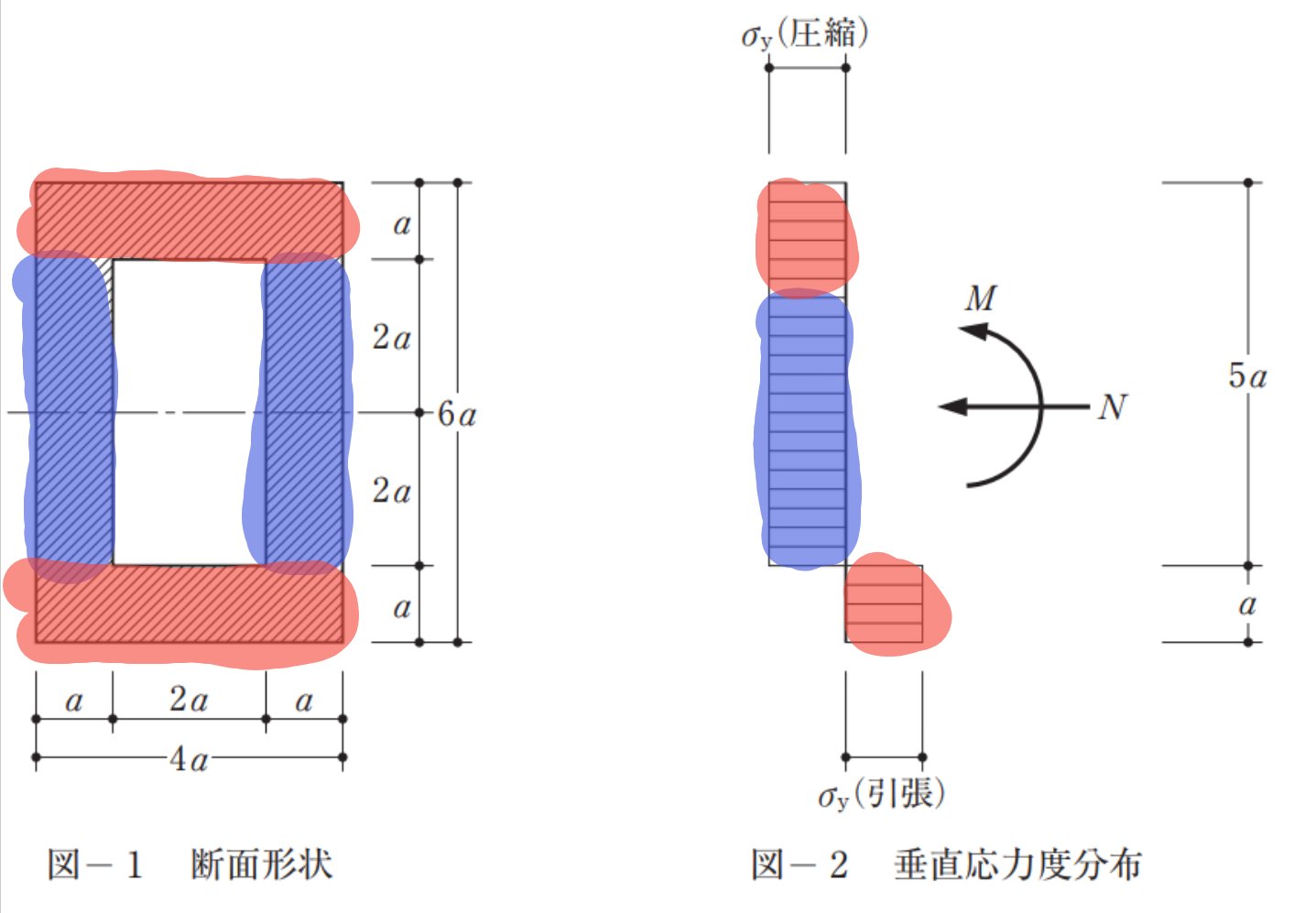
Nの部分の面積を求めると
4a×2a=8a2
なので、
N=8a2σy
となります。
一方でMの上の部分の面積を求めると
a×4a=4a2
なので、引張から圧縮までの距離5aをかけると、
M=4a2×5aσy=20a3σy
です。
よって答えは4番となります。
まとめ
この記事では、「全塑性モーメントとかムズすぎ。どうやったら計算できるの?」
こんな疑問にお答えしました。
まとめると、公式は簡単に覚えられますが解き方が肝になるので覚えましょう。
この記事を参考に、素敵な構造計算ライフをお過ごしください。









